资料获取:电机控制资料获取
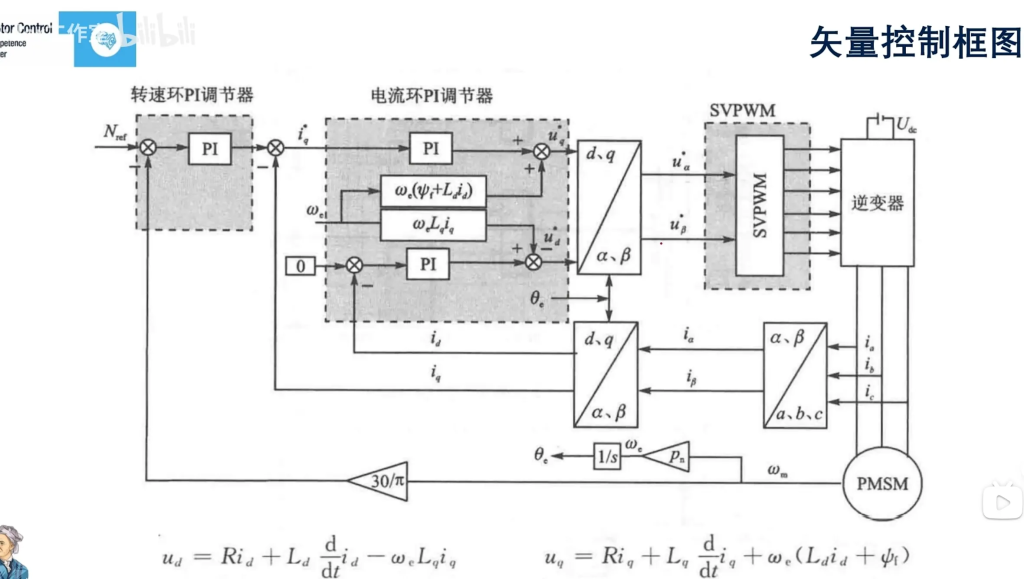
矢量控制框图
克拉克变换与逆运算
克拉克变换
我们知道,交替开关的MOS管可以实现电机的转动,而这些交替开关的MOS管是以极其快的速度在周期性进行的,把这些周期性的开启和关断过程联系起来,并且对其各个相进行单独观察,就可以得到三个相A、B、C的电流随时间变换的曲线,如下图所示,他们之间存在120°的相位差。
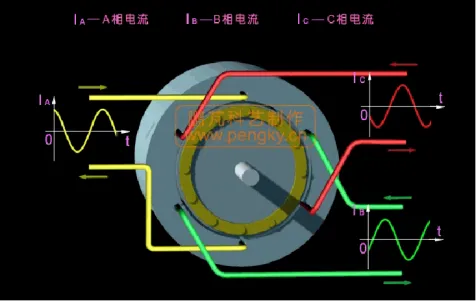
换一个角度来思考此问题,实际上,我们只要能够控制这个相位差为120°的sin状波形,就能够实现针对电机的控制。
而克拉克变换就是实现这个波形控制的第一步。
我们知道,虽然说是要控制120度的sin状型波形来实现电机控制,但是只要仔细想一想,就会知道这个波形其实是极难控制和改变参数的。首先相与相之间是相互耦合的,MOS管一打开就会至少同时打开两个相,所以只想改变一相来实现电机控制是肯定不行的,必须得三相捷联起来一起改变,才能够实现电机的控制。所以,实现电机控制的问题就会变成很复杂。
显然,人的本性不容许我们把问题进一步复杂化,因此,我们需要对这个问题进行降维,尽量把这个多变量耦合的问题降解为最好是单一变量的控制问题,克拉克变换就是想做这件事。
所谓克拉克变换,实际上就是降维解耦的过程,把难以辨明和控制的三相相位差120°电机波形降维为两维矢量。
它的思路其实特别的简单,第一就是把三相随时间变换的,相位差为120°的电流波形抽象化为三个间隔120°的矢量。
第二就是利用三角函数对矢量进行降维,降维到两个坐标轴,从此复杂的三相变化问题就降解为了α-β坐标轴的坐标上的数值变化问题。
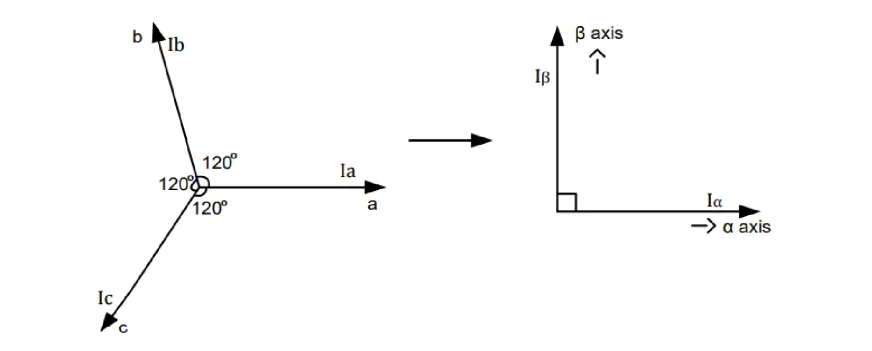
上图中,左边是我们把三相120度相位差的sin状波形抽象化为矢量之后的样子,而右边就是我们需要把这三个矢量进行投影的坐标轴。只要我们把三个矢量都投影到坐标轴上,那么,一个三矢量问题就变成一个二维坐标平面问题。
下面我们来进行一次投影过程的详细推导。
万恶之源的开始,就是三角函数:
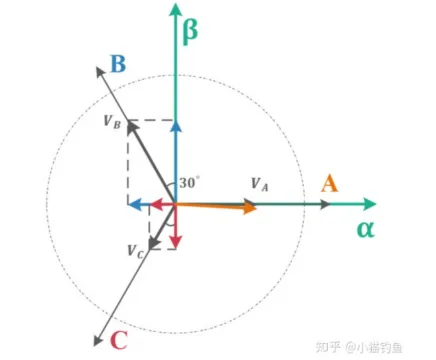
显然,针对α-β坐标系中α轴,有:
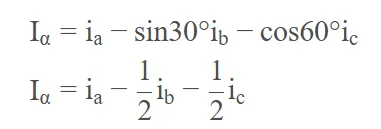
针对α-β坐标系中β轴,有
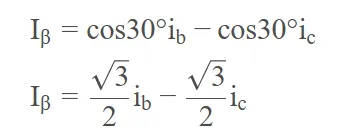
把上面的投影结果列成矩阵形式,有:
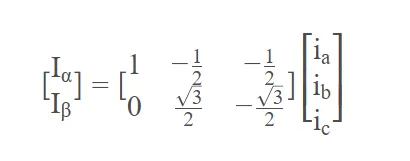
这就是克拉克变换的第一步,作投影。
上面的步骤都很简单,但是我们会发现,往往最终论文或者资料上克拉克变换的体现形式都不是上面这样子,而是会加上一个系数,如$\frac{2}{3}$(等幅值变换系数),或者$\sqrt{\frac{2}{3}}$(等功率变换系数)。分别对应两个变换方式,分别为等功率(系数:$\sqrt{\frac{2}{3}}$)变换方式和等幅值(系数:$\frac{2}{3}$)变换方式。这里仅讨论等幅值变换加上系数后,原本的投影式变为:
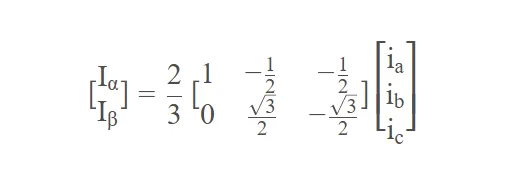
这就是克拉克变换的等幅值形式。
何为等幅值变换?用α相电流输入1A电流的特例来举例,当电流输入时候,根据基尔霍夫电流定律(电路中任一个节点上,在任意时刻,流入节点的电流之和等于流出节点的电流之和,如下图),有:
ia+ib+ic=0
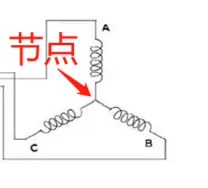
设定ia为-1,则根据上面的式子,有ib和ic为1221,列成矩阵形式后,如下所示:
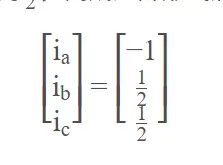
将这个ia,ib,ic的参数带入到我们上面的 直接投影式子中,得到:
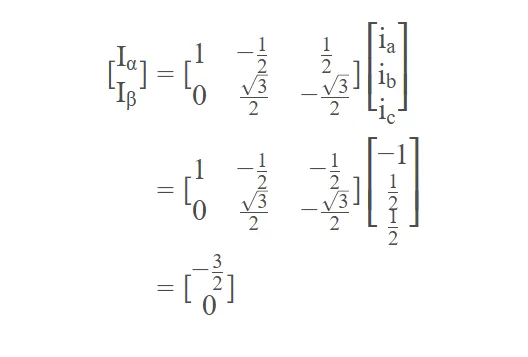
这就看出问题了,显然,尽管矢量a与α轴重合,但是由于b,c相电流投影的存在,导致在a相输入1A电流,反应在α轴上的电流并不是等赋值的1A,而是−3/2。
因此,为了让式子等辐值,即使得a相1A时,反应在α轴上的电流也是1A,我们就得乘上系数2/3,针对上面的投影式乘上2/3后,式子变换为:
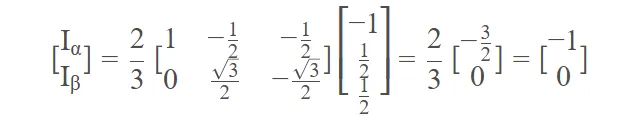
这就是克拉克变换的等幅值表现形式。
基于等赋值变换,我们就能够得到α、β相位与ia,ib,ic的关系,已知等赋值变换式:
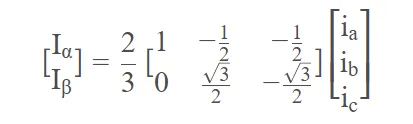
移项
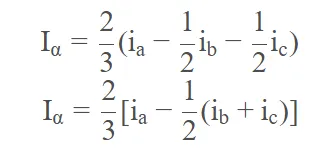
又根据上面所提到的基尔霍夫电流定律:
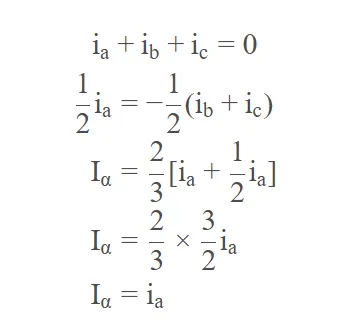
通过上述步骤,成功推导Iα=ia。 进一步的,可求Iβ,已知:
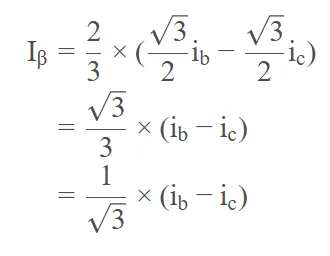
又根据上面所提到的基尔霍夫电流定律:
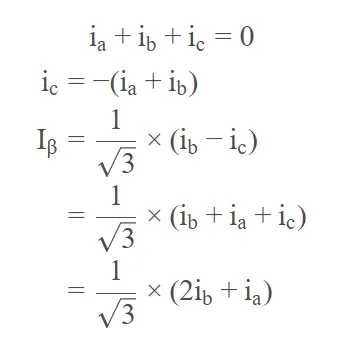
综合上述步骤,我们已经得到了列出ia,ib,ic电流与Iα,Iβ电流的关键关系式,总结如下:
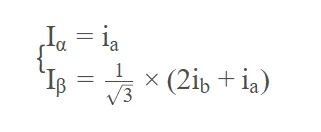
可以看出,在式子中,我们消去了变量ic,这是因为由于基尔霍夫电流定律的存在,我们并不需要知道所有三相电流,我们只需要知道两相电流就能够求解得到另外一相的电流,反映在硬件上,我们就可以省去一路的电流传感器!节省了成本!
克拉克逆变换
我们已经知道了克拉克变换后的Iα、Iβ,我们在此基础上研究克拉克逆变换,首先,ia的逆变换我们是不需要研究的,因为我们已经知道了Iα=ia。
进一步的,我们研究逆变换ib:
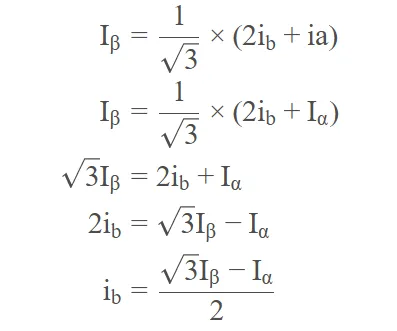
最后,还是根据基尔霍夫电流定律:ia+ib+ic=0,我们得到逆变换ic:
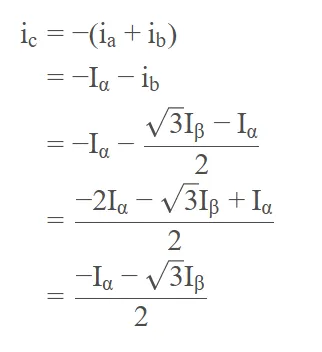
则克拉克逆变换三式皆得,总结如下:
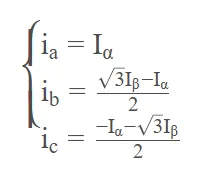
帕克变换与反帕克变换
帕克变换
由克拉克变换,实际上我们已经成功对电机的正弦驱动三相曲线进行降维度,使之变成了一个两轴坐标问题,并且得到其转换关系。但是只有它是不够的,我们还需要将这个理论和旋转电机对应起来,也就是建立电机旋转时的数学模型。
我们需要知道能够使得电机旋转的IαI和Iβ电流输入规律,如果我们可以知道这个能够使得电机旋转的Iα和Iβ电流输入规律,我们就可以通过克拉克逆变换,把这个旋转情况下的Iα和Iβ逆变换为ia,ib,ic三相电流波形,从而就实现了用把ia,ib,ic降维后的IαIα和IβIβ实现对电机的控制,那么问题就没有原来我们想的直接控制ia,ib,ic来控制电机旋转来得复杂了。
帕克变换就是能够帮助我们求得各种旋转情况下的Iα和Iβ。
其实整个帕克变换的思路很简单,首先,我们把电机的定子线圈上固定一个Iα−Iβ坐标系,如下图左边的图所示,这时候,我在坐标系的右边放上一个转子,如下图右边所示,如果此时转子被吸引且不动,那么在Iα−Iβ坐标系中就一定有一个Iα和Iβ值是能够对应转子现在的状态的。
但是,显然,我们的问题不是不动那么简单,在实际的应用中,我们的转子是在转动的,因此,对应转子状态的IαIα和IβIβ值实际上在一直变化,变化的东西是不好描述而且是讨厌的,如最开始,我们很讨厌ia,ib,ic三相相位差120°的变化波形,我们用克拉克变换对它进行了降维描述。
可是在这里,我们发现降维后尽管少了一个变量,但是只要电机转动,Iα和Iβ就依然在一直变化,依然很讨厌,那么这时候,懒惰的人类就又开始想办法,有没有办法能够用一个定值来描述无刷电机的旋转呢?也就是说,能不能对这个电机系统进行进一步的降维,使得我们甚至不用考虑变化的Iα,Iβ只需要有一个定值就能够描述整个电机系统的转动状态?
答案是有!帕克变换就是想带我们做这件事!!
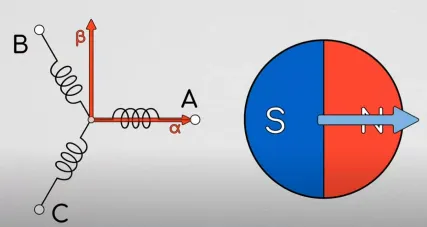
帕克在我们刚刚固定在电机定子上的Iα−Iβ坐标系上,另外新建了一个坐标系,我们称之为Iq−Id坐标系,这个坐标系是可以随电机转子转动的!它与电机转子固联!!如下图所示:
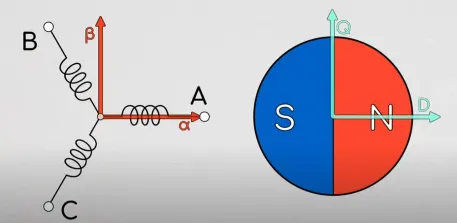
那么我们就有了两个坐标系了,一个是固定在定子上的坐标系Iα−Iβ,一个是固定在转子上的坐标系Iq−Id。
进一步的,我们把两个坐标系画在一起,我们就有如下图所示的坐标:
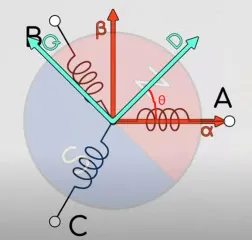
其中,Iq−Id坐标系随转子转动,D轴在此处设定为指向电机的N级,Iq−Id坐标系因转动而造成的与Iα−Iβ坐标系的差角θ,就被称为电角度!
那么,很轻松的,还是利用简单的三角函数构建的旋转矩阵,在知道电角度的前提下,我们很容易就能够把iq−id坐标系上的值映射(旋转)到iα−iβ坐标系上!式子如下:
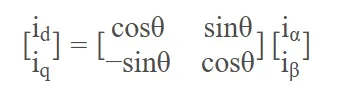
因此,在知道电角度的前提下,我们就可以用iq,id坐标系上的定值来描述电机的旋转!这正是我们一直渴望的电机旋转数学模型!
反帕克变换
根据矩阵乘法,取逆,我们可进行帕克逆变换,也就是知道iq,id值和电角度的前提下,反求iα,iβ式子如下:
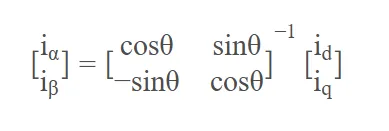
写成等式结果:
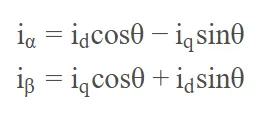
在实际的FOC应用中,电角度是实时有编码器求出的,因此是已知的。Iq和Id可以合成一个矢量,加上电角度(旋转)的存在,因此可以看成一个旋转的矢量。在通过Iq,Id和电角度求得Iα和Iβ后,我们就可以通过前面提到的克拉克逆变换求得ia,ib,ic的波形,这正是FOC的基本过程!
通常在简单的FOC应用中,我们只需要控制Iq的电流大小,而把Id设置为0。此时,Iq的大小间接就决定了定子三相电流的大小,进而决定了定子产生磁场的强度。进一步我们可以说,它决定了电机产生的力矩大小!
而iq是旋转的矢量;在前面说了,同时Iq又会间接影响磁场的强度,这正是FOC的名称磁场定向控制的由来。
励磁和力矩:d、q轴电流的不同

如图所示,d轴电流平行于永磁体磁场方向,q轴电流正交于永磁体磁场方向。
那么d轴的电流可以用于磁化或消磁永磁体(并不是真的消磁,而是d轴电流本身产生的磁场可以抵消永磁体的磁场);
q轴的电流可以用于产生使磁体旋转的力矩。
在控制中,我们通常把$U_d$控制在0,只保留$U_q$。


发表回复