资料获取:电机控制资料获取
线性定常微分方程求解
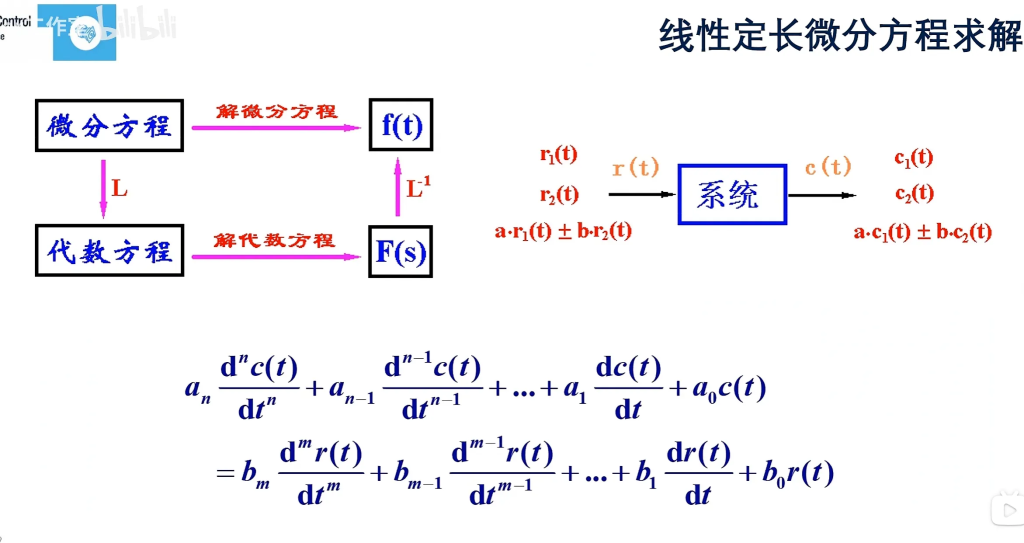
什么是线性定常微分方程?
线性:af(x)=f(ax);
f(x1)+f(x2)=f(x1+x2)
定常:方程的系数不随时间变化
除此之外还有复数的概念、欧拉公式等知识点,请自行查阅资料。后文如果在哪里用到这些知识我会尽量指出来的。
拉普拉斯变换
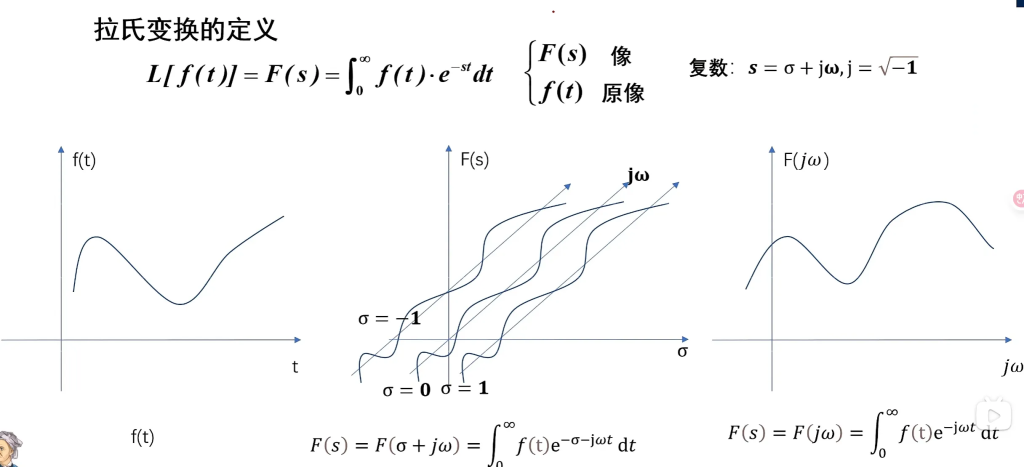
定义:$F(s) = \int_0^{\infty} f(t) \cdot e^{-st} dt$,其中s为复数。
拉普拉斯变换分为单边拉普拉斯和双边拉普拉斯,区别在于它们的积分下限是否包括0~-∞。在控制领域中由于时间很少为负数,所以用的都是单边变换。
如此变换过后,原本二维的图像变成了三维,以F(s)为Z轴的一个三元函数。特别的,当σ=0时,F(s)=F(jω)(第三个图),F(s)与jω形成一个复平面。(实际上,σ=0是拉普拉斯变换的一个特例,它又叫傅里叶变换)


传递函数
递函数是线性定常系统在零初始条件下,输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。求传递函数的核心是将系统的微分方程进行拉普拉斯变换,再整理成$G(s)=\frac{Y(s)}{U(s)}$的形式。
如何得到传递函数
首先利用拉普拉斯变换的线性性质和微分性质:
- 线性性质:$\mathcal{L}{af(t)+bg(t)}=a\mathcal{L}{f(t)}+b\mathcal{L}{g(t)}$;
- 微分性质:$\mathcal{L}{\frac{df(t)}{dt}}=sF(s)-f(0)$,在零初始条件($f(0)=0$)下,$\mathcal{L}{\frac{df(t)}{dt}}=sF(s)$,
对系统的输入和输出方程做变换(以震荡电路为例):
RC电路
- 输入:电压源$u(t)$;
- 输出:电容电压$y(t)=v_C(t)$;
- 微分方程:$RC\frac{dy}{dt}+y = u$。
对RC电路微分方程变换:
- 左边:$\mathcal{L}{RC\frac{dy}{dt}+y}=RCsY(s)+Y(s)$;
- 右边:$\mathcal{L}{u}=U(s)$。
将拉普拉斯变换后的方程变形,得到传递函数。
RC电路传递函数:
- $RCsY(s)+Y(s)=U(s)$;
- 提取$Y(s)$:$Y(s)(RCs + 1)=U(s)$;
- 解得:$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{RCs + 1}$。
传递函数的意义(拉普拉斯逆变换)
对传递函数做逆变换即可回到原系统方程。具体过程见下“传递函数的意义(极点)”
传递函数的意义(极点)
极点就是传递函数分母为0时求得的s的值。
如一个系统的传递函数为$G(s)=\frac{s + 2}{s + 1}$,当s+1=0时,s=-1为该传递函数的极点。
不过大部分情况我们的传递函数长这样:${\Large G(s)=\frac{1}{s^2+2s+2}=\frac{\frac{1}{2i}}{s + 1 – i} + \frac{ \frac{-1}{2i}}{s + 1 + i}}$,(因式分解)
解得:$\begin{cases} s_1=-1+i \\ s_2=-1-i \end{cases}$
如果我们对G(s)做逆变换,得:
$\begin{align}\mathcal{L}^{-1}[G_{(s)}]&= \mathcal{L}^{-1} \left[ \frac{1}{2i} \cdot \frac{1}{s + 1 – i} + \frac{-1}{2i} \cdot \frac{1}{s + 1 + i} \right]\\ &= \frac{1}{2i} e^{(-1+i)t} – \frac{1}{2i} e^{(-1-i)t}\\ &= \frac{1}{2i} e^{-t} (e^{it} – e^{-it})\\ &= \frac{1}{2i} e^{-t} (\cos t + i \sin t – (\cos t – i \sin t))\\ &= \frac{1}{2i} e^{-t} (2i \sin t)\\ &= e^{-t} \sin t \end{align}$
其中第三行到第四行用到了欧拉公式:$e^{ix} = \cos x + i \sin x$。
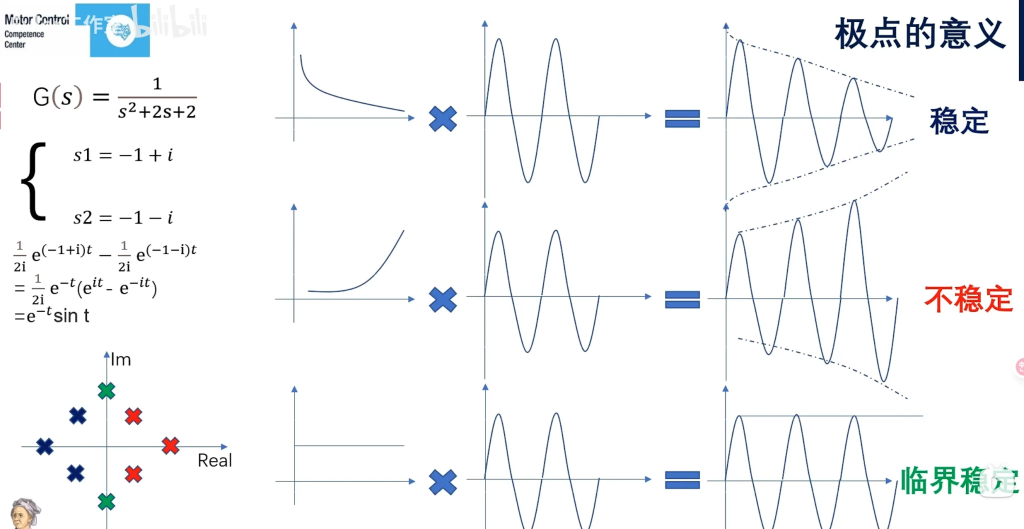
从逆变换过程(具体来说是第二行$\frac{1}{2i} e^{(-1+i)t} – \frac{1}{2i} e^{(-1-i)t}$)可以看到,极点的实数部分决定了最终结果是$e^{t}$还是$e^{-t}$,而这有决定了最终结果($e^{-t} \sin t$)是发散还是收敛。我们的目标是做一个控制系统,那当然希望这个系统是稳定(收敛)的,而不是不稳定或临界稳定的。
事实上,当实数部分<0时,系统稳定;
>0时,系统不稳定;
=0时,系统临界稳定。(见左下角坐标系示意图)


发表回复