嵌入式合集（需要语雀账户，建议黑色配色阅读）

资料获取：电机控制资料获取

有关PID控制的基础部分，详情见PID控制算法

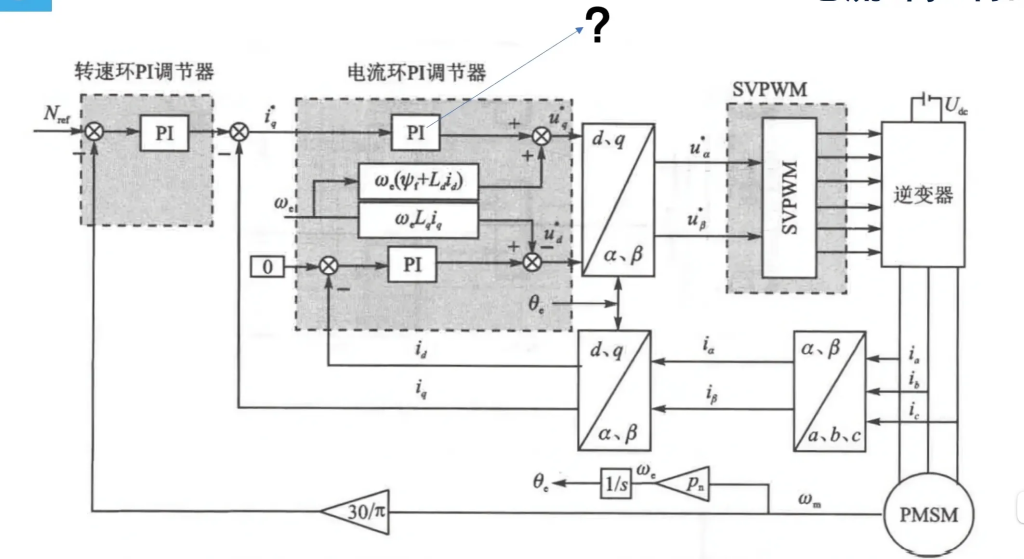
电流环控制器

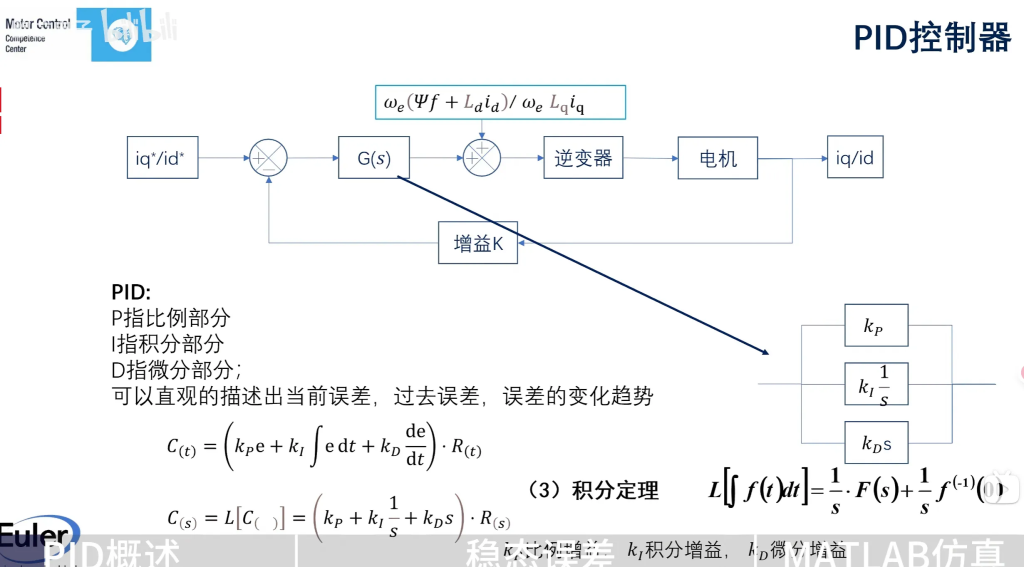
这是通常情况下的PID公式：$C(t) = \left( k_P e + k_I \int e \, dt + k_D \frac{de}{dt} \right) \cdot R(t)$

对它做拉普拉斯变换(用到了积分定理)：$C(s) = L\left[ C(t ) \right] = \left( k_P + k_I \frac{1}{s} + k_D s \right) \cdot R(s)$

P控制器

传递函数推导

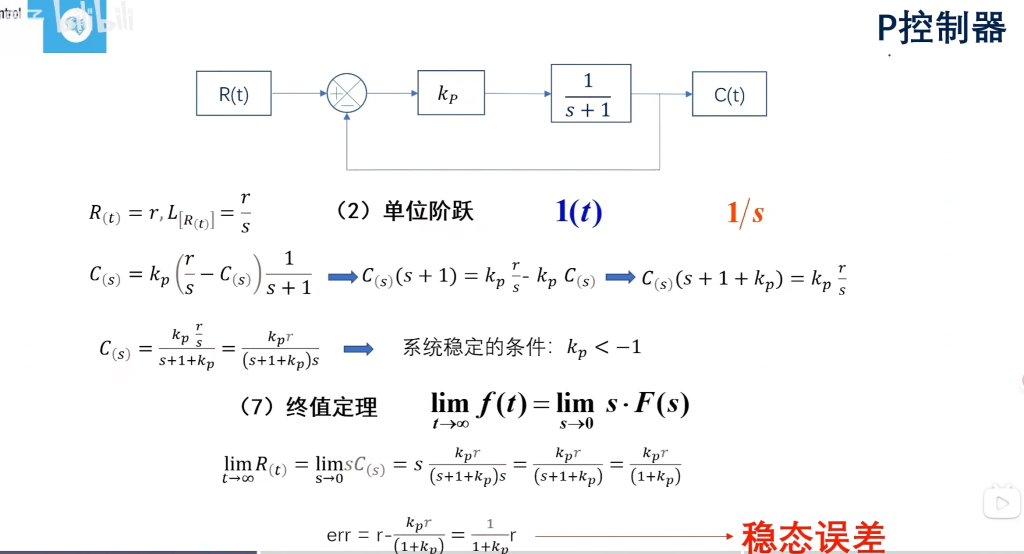
通常情况下，我们总是希望控制系统保持一个不变的输出值，也就是说R(t)是一个常数r；

在只有P项的情况下，PID公式为$C(t)=k_Pe$,它在拉普拉斯变换后为：$C(s) = k_P e$,其中$e=R(t)-C(t-1)$,即期望与上一次PID输出之差；

我们假设被控对象传递函数为$G(s)=\frac{1}{s+1}$；

那么整个系统的开环传递函数为：

$ \begin{align} G_{open}(s)&=C(s) \cdot G(s)\\ &=\frac{k_p\frac{r}{s}-k_pC(s)}{s+1}\\ &=\frac{k_pr}{(s+1+k_p)s} \end{align}$

开环传递函数推导：

• PID 控制器传递函数 $G_{pid}(s)=k_p + k_i\frac{1}{s}+k_d s$是根据 PID 控制规律 $u(t)=k_p e(t)+k_i\int e(t)dt + k_d\frac{de(t)}{dt}$进行拉普拉斯变换（假设 e(0)=0 等初始条件为零）得到的，其中 u(t) 是控制器输出，e(t)是误差信号。
• 被控对象传递函数 $G(s)=\frac{1}{s + 1}$描述了被控对象在拉普拉斯域的输入输出关系。开环传递函数表示控制器输出直接作用于被控对象时的传递关系，所以将两者相乘。
• 对乘积 $\left(k_p + k_i\frac{1}{s}+k_d s\right)\times\frac{1}{s + 1}$ 进行通分展开，就得到了$\frac{k_p}{s + 1}+\frac{k_i}{s(s + 1)}+\frac{k_d s}{s + 1}$。

求极点得$\begin{cases}s=0\\ s=-k_p-1\end{cases}$,要想让系统达到稳态s必须处于负半轴，解得$k_p>-1$(所以图中说小于-1标错了)

稳态误差

根据拉普拉斯终值定理：$\lim_{t \to \infty} f(t) = \lim_{s \to 0} s \cdot F(s)$ ,

所以:

$\begin{align} \lim_{t \to \infty} R_{(t)} = \lim_{s \to 0} s C_{(s)} &= s \frac{k_p r}{(s + 1 + k_p)s}\\ &= \frac{k_p r}{(s + 1 + k_p)}\\ &= \frac{k_p r}{(1 + k_p)}\end{align}$

即当时间趋于无穷时，最终系统达到稳态，此时输出值为$\frac{k_p r}{(1 + k_p)}$。

所以$err=r-\frac{k_p r}{(1 + k_p)}=\frac{1}{1+k_p}r$就是整个系统的稳态误差。

仿照上述过程，试着推导一下，当被控对象满足什么条件时，系统不会有稳态误差？

PI控制器

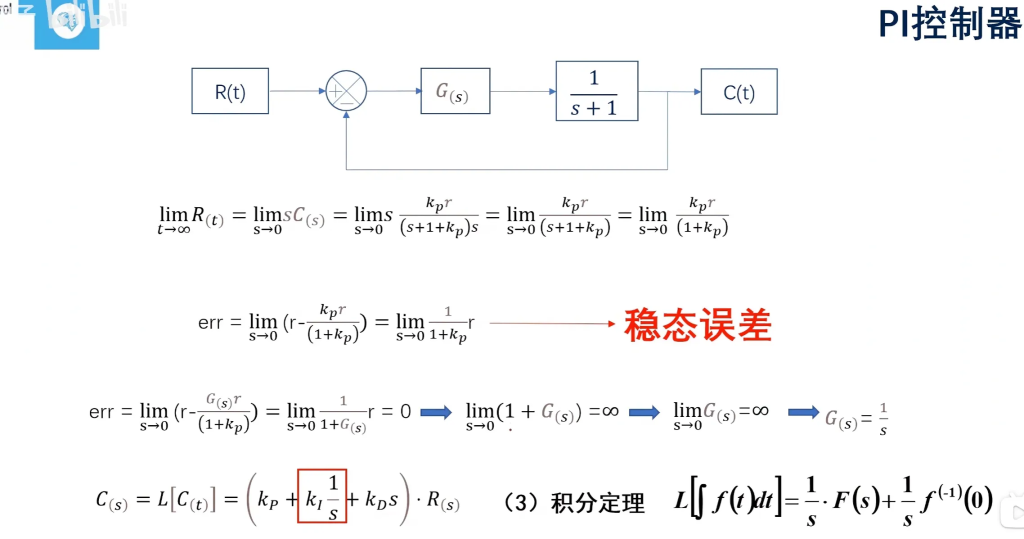
添加I项以后，PID在拉普拉斯域的表达式为：$C(s) = \left( k_P + k_I \frac{1}{s} \right) \cdot R(s)$。

我们先接着上面P项的结论来继续探讨：目前我们的控制系统有个稳态误差，但是我们不希望出现这个稳态误差，说明当前的控制系统无法满足我们的需要。

于是我们先假定一个新的控制系统，它的传递函数是G2(s)，和我们的P控制器共同控制系统。

所以这个新的系统的传递函数为：$G_{system}(s)=G_2(s) \cdot C_{P}(s) \cdot G(s)$;

其中Cp(s)是P控制器传递函数，G(s)是我们假设的被控对象的传递函数。

在这种情况下，想让err=0，即：

$err = \lim_{s \to 0} \left(r – \frac{G_2(s)r}{(1 + k_p)}\right) = \lim_{s \to 0} \frac{1}{1 + G_2(s)} r = 0$

解得$G_2(s)=\frac{1}{s}$满足要求（满足$\lim_{s \to 0} G_2(s)= 0$的函数有很多，但是根据简洁的原则，1/s是最容易想到的一个解）。

而根据积分定理我们便可以逆变换出I项了。

PID控制器

高频噪声

虽然PI控制器已经可以将系统的稳态误差消除了，已经初步满足我们的要求了，但是引入I项会使系统达到稳定的时间延长，并伴随着超调的风险；这时候是不是可以靠引入D项来解决呢？

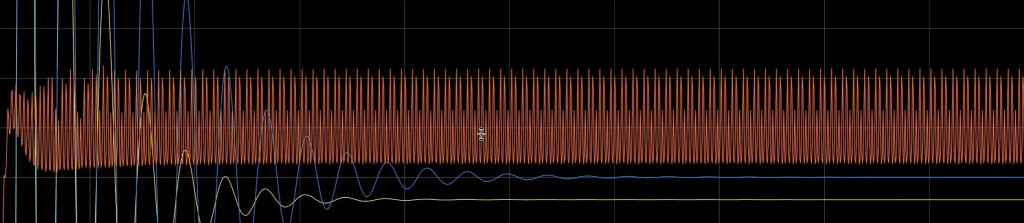
但我们可以看到，加入D项后，整个系统的波形变得像是混合了某种噪声一样。

事实上，这种噪声来自于整个环境，即便是幅值非常小的噪声，如果频率很高的话，对PID控制器的影响将是灾难性的（P和PI要好一点，但即便如此也会使其期望值翻了10倍）

为什么不用PID控制器

固然，来自环境的高频噪声可以用低通滤波器来解决：

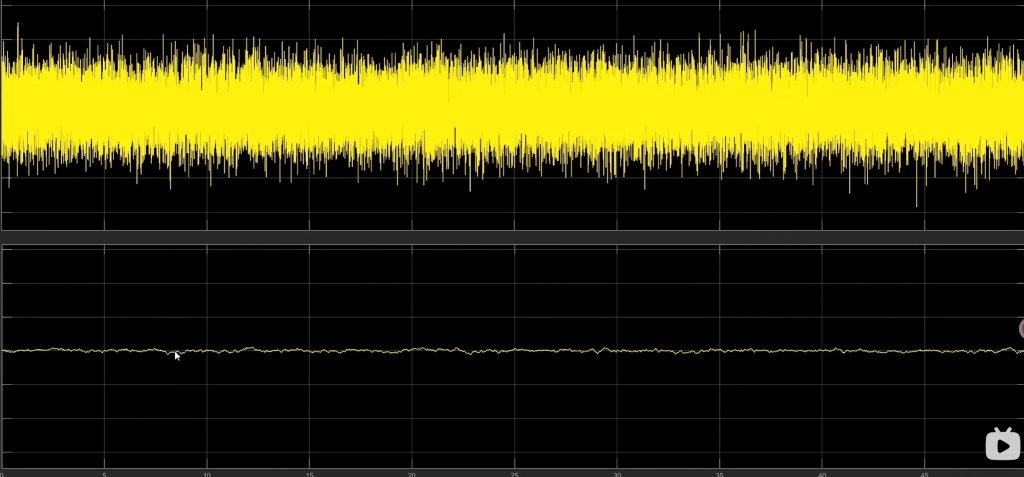
但这样会使我们本就不富裕的MCU算力雪上加霜；所以通常情况下使用PI控制器来控制电流环已经足够了。

电流环PI参数计算

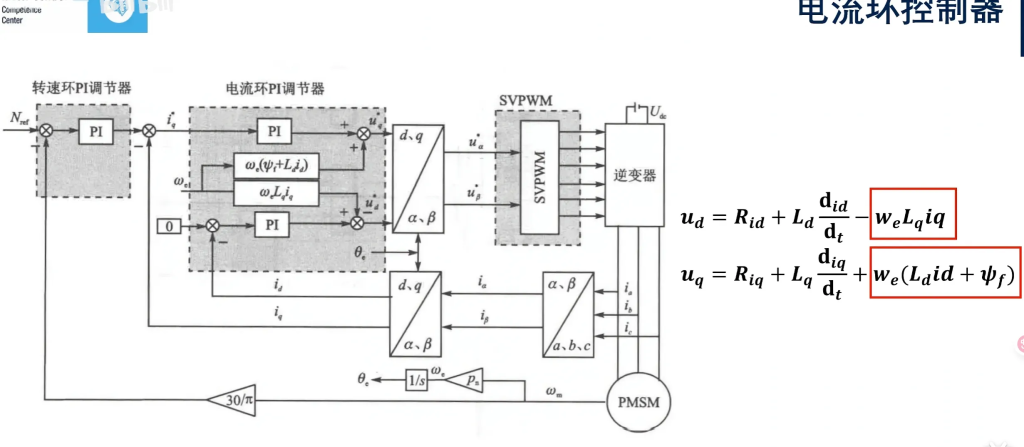
电流环闭环传递函数

电机数学模型（dq轴）：$\begin{cases} u_d = R i_d + L_d \frac{\mathrm{d} i_{id}}{\mathrm{d} t} – \boldsymbol{w_e L_q iq} \\ u_q = R i_{iq} + L_q \frac{\mathrm{d} i_{iq}}{\mathrm{d} t} + \boldsymbol{w_e (L_d id + \psi_f)} \end{cases}$

前面我们说过，想要做拉普拉斯变换，必须得是一个线性定常的系统才行。但是不论d轴还是q轴，其表达式末尾都有一个常数项，这就不满足“线性”的要求了。

于是我们在调控时，先忽略这一部分，在PI控制器调控完后再当作前馈加上去（就像框图里做的那样）。

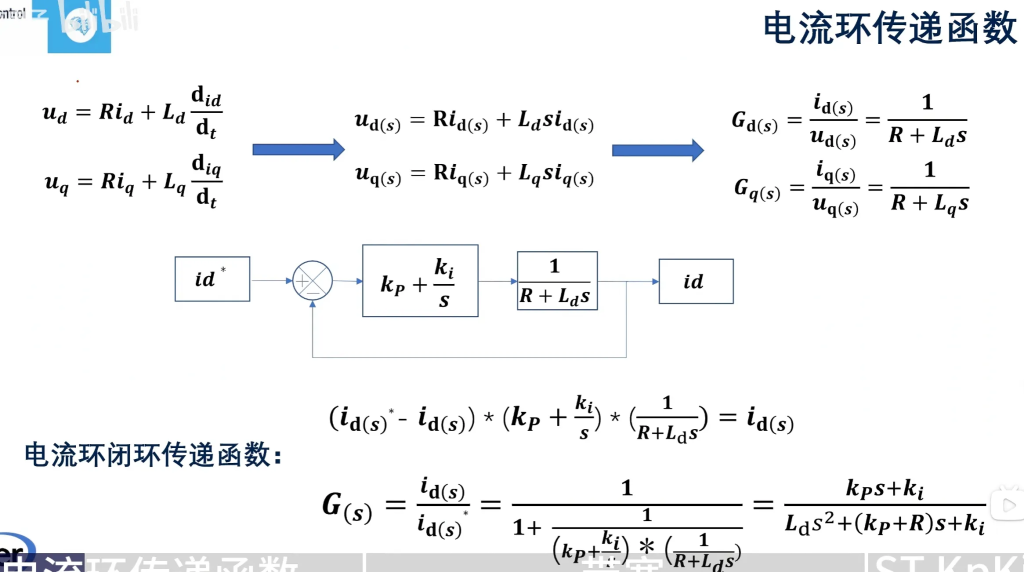
此时将dq轴做拉普拉斯变换：$\begin{cases} u_{d}(s)=R i_{d}(s)+L_d s i_{d}(s)\\ u_{q}(s)=R i_{q}(s)+L_q s i_{q}(s) \end{cases}$

可得传递函数：

$\begin{cases}\Large G_{d}(s)=\frac{i_{d}(s)}{u_{d}(s)}=\frac{1}{R + L_d s}\\ \Large G_{q}(s)=\frac{i_{q}(s)}{u_{q}(s)}=\frac{1}{R + L_q s} \end{cases}$

然后看图片中间部分，这是我们调控id时的框图，系统输入期望值id*，输出调控值id；

有：$\left( i_{d}(s)^{*}-i_{d}(s) \right)\left( k_P+\frac{k_i}{s} \right)\left( \frac{1}{R + L_d s} \right)=i_{d}(s)$

整理可得：$G(s)=\frac{i_{d}(s)}{i_{d}(s)^{*}}=\frac{1}{1+\frac{1}{\left( k_P+\frac{k_i}{s} \right)\left( \frac{1}{R + L_d s} \right)}}=\frac{k_P s + k_i}{L_d s^2+(k_P + R)s + k_i}$

我们发现分母有个二阶的s，这肯定是不利于我们求解的，于是还要进一步处理；除了求根公式和因式分解以外，我们还有一种方法：

通过带宽计算参数

令：$\begin{cases}k_p=L_d\omega_c\\ k_i=R\omega_c \end{cases}$,其中ωc为电流环带宽。

什么是电流环带宽？

电流环带宽是指电流环的闭环系统频率响应中，幅值衰减到低频（通常取 ω=0 时的幅值作为参考）幅值的 $\frac{1}{\sqrt{2}}$（约 0.707 倍）时所对应的频率 ωb。也就是说，当输入信号频率低于 ωb 时，电流环能够较好地跟踪输入信号（幅值衰减较小，相位滞后也较小）；而当输入信号频率高于 ωb 时，电流环对输入信号的跟踪能力显著下降。

带宽并不是越大越好：带宽越大，受到环境噪声的干扰就越多。

如何计算带宽？

• 假设电流环的闭环传递函数为 $G_{closed}(s)$（通过对电流环的控制器（如PI控制器）、被控对象（如电机的电枢回路等）进行拉普拉斯变换和闭环系统分析得到）。
• 令 $s = j\omega$（j 是虚数单位），代入 $G_{closed}(s)$ 得到频率响应 $G_{closed}(j\omega)$。
• 计算 $|G_{closed}(j\omega)|$（幅值响应），当 $|G_{closed}(j\omega)|=\frac{|G_{closed}(j0)|}{\sqrt{2}}$ 时，对应的 ω 就是电流环带宽 ωb。例如，若电流环闭环传递函数 $G_{closed}(s)=\frac{k_{PS}+k_i}{L_d s^2+(k_P + R)s + k_i}$（类似于一些简单电机电流环模型的传递函数形式，其中 kP、ki 是PI控制器参数，Ld 是电感，R 是电阻），将 s=jω 代入后，通过计算幅值并找到满足上述幅值条件的 ω 值，即可确定带宽。
• 第二种方法：令τ=min{Ld/R,Lq/R}，ωc=2Π/τ；

所以：

$\begin{align} G_{(s)}=\frac{i_{d(s)}}{i_{d(s)}^{*}}&=\frac{k_{P}s + k_{i}}{L_{d}s^{2}+(k_{P}+R)s + k_{i}}\\ &=\frac{L_{d}\omega_{c}s+R\omega_{c}}{L_{d}s^{2}+(L_{d}\omega_{c}+R)s + R\omega_{c}}\\ &=\frac{\omega_{c}}{s+\omega_{c}} \end{align}$

• 其中最后一步需要的分母因式分解得到。

依据 $\begin{cases}τ=\min(\frac{L_d}{R},\frac{L_q}{R})\\ ω_c=\frac{2\pi}{\tau}\end{cases}$ 计算出ωc，并代入 $\begin{cases}k_p=L_d\omega_c\\ k_i=R\omega_c \end{cases}$ 即可算出Kp、Ki的值。

同理，q轴公式为$\begin{cases}k_p=L_q\omega_c\\ k_i=R\omega_c \end{cases}$ 。

速度环控制器

一般来说速度环控制器的带宽时电流环的5~10分之一。但是还千万别以此为依据去否定其它的参数，比如我在实际建模后发现1/20才是最优解。

计算公式：

$\begin{cases}k_{p\omega}=\frac{\beta J}{1.5p_n\phi_f}\\k_{iw}=\beta k_{pw}\end{cases}$

，其中β为速度环带宽，Pn为电机极对数，Φf为磁通量，J为电机转动惯量。