STM32G0/G4驱动BLDC/PMSM电机——第六讲：SVPWM

9 月 5, 2025

—

由

文止墨

于嵌入式, 文章, 编程

嵌入式合集（需要语雀账户，建议黑色配色阅读）

资料获取：电机控制资料获取

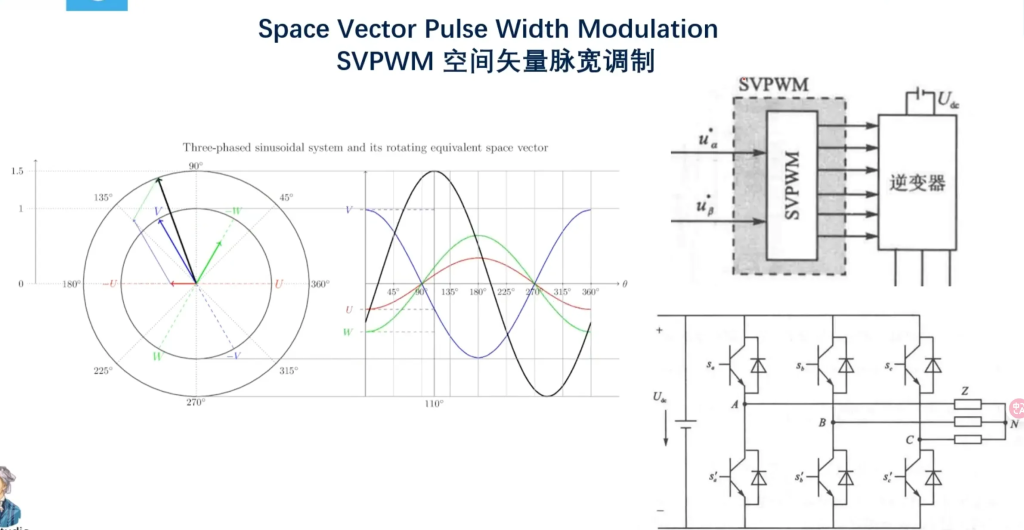
SPWM和SVPWM介绍

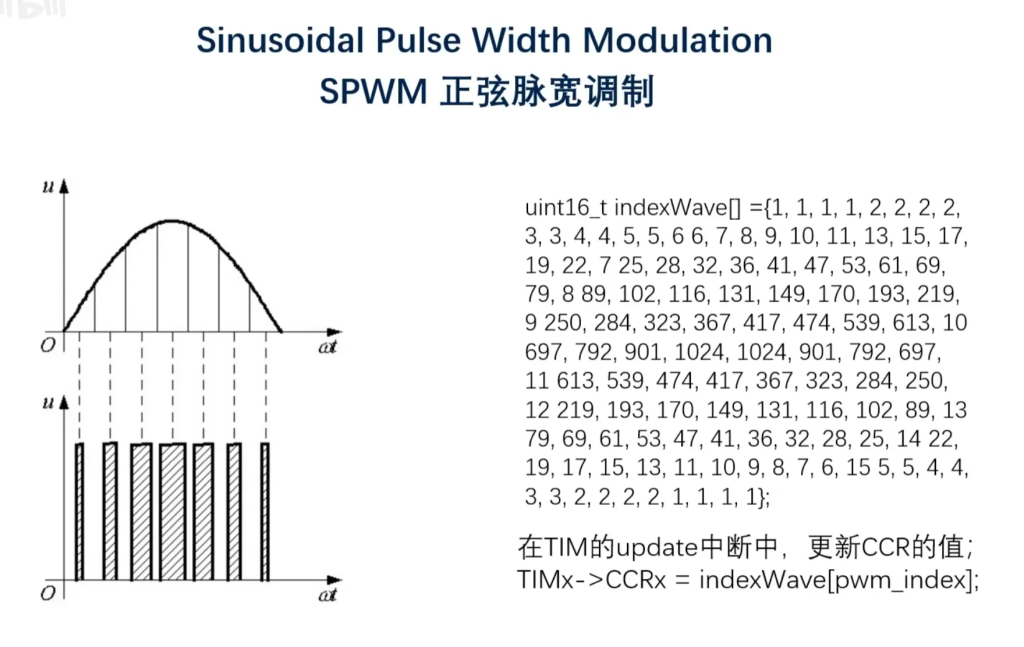
做过呼吸灯的应该都很清楚这个过程吧……

控制逻辑

由于我们通常使$U_d$保持为0，所以我们需要的参数只有$U_q$（所需力矩电压）和$\theta$（电机当前角度）;将这些参数用反帕克变换和反克拉克变换后成为$U_a U_b U_c$,再由逆变器输出相应电压控制电机旋转。

其实真正的算法应该接收Uα和Uβ作为参数。

最后：$\vec {U_{out}} = \vec {U_a}+\vec {U_b}+\vec {U_c}$

矢量合成

如图，只要我们像正弦脉宽调制那样调制各个mos管，就可以输出我们想要的电压，进而产生对应的力矩了。

这个过程简单解释就是我们已经知道了ABC对应三个方向的向量，通过SPWM分别调整这三个向量的模长，就可以矢量合成出不同的方向向量了。

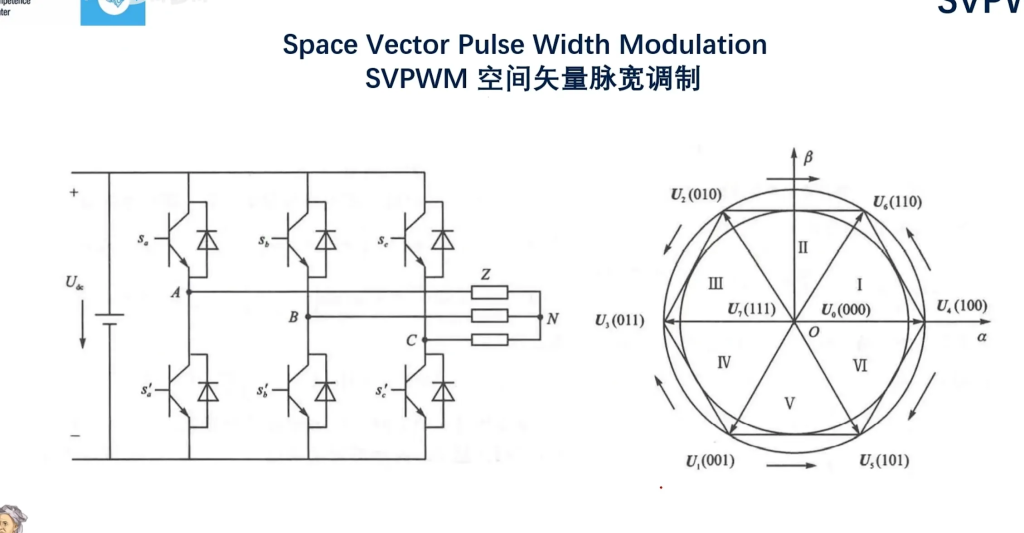
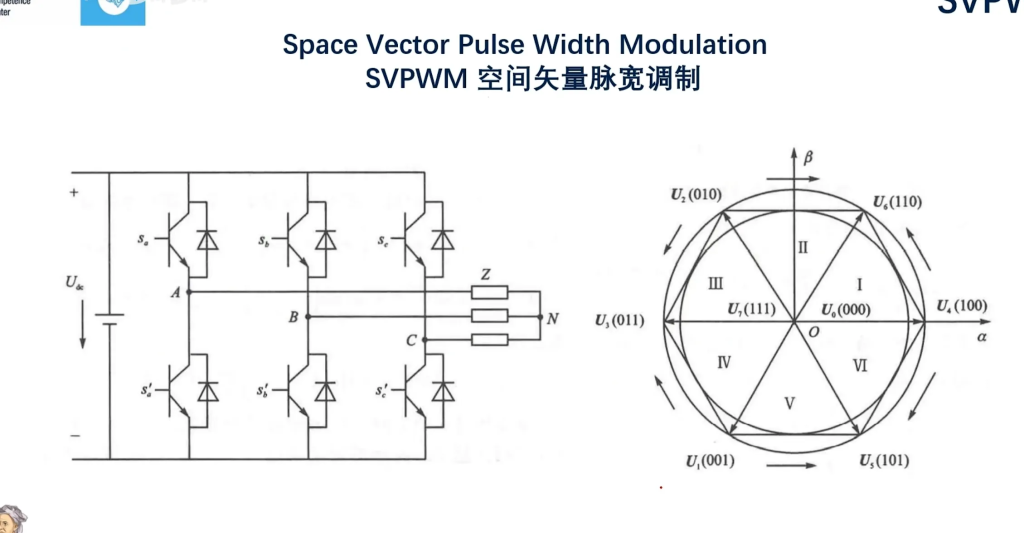
我们前面在第五讲：SVPWM引入的时候说过STM32只能输出正电压，这也是为什么我们有三个mos管而不是两个的原因（理论上两个不平行的向量足以表示该平面所有向量了，但由于没有负值，所以我们需要一个额外的方向相反的向量，就比如图中的U1就是U6的相反向量）

SVPWM算法原理

什么是调制比？

简单来说就是输出电压值与输入值之比。

SPWM的最高值就是输入值，所以它的M为1；

SVPWM的输出值因为可以由多个矢量合成，因此最高值会比输入值高，如下图的U。

AI解释调制

1概念：到底在“调制”谁？

逆变器最终想输出的是低频正弦电压（基波），但功率器件只能“开/关”。
解决思路：用高频开关信号（载波）去“搬运”一个低频目标波形（调制波）。
因此：
调制波 = 低频目标电压波形
载波 = 高频三角/锯齿波或定时比较器
调制动作 = 把目标波形“叠”到载波上 → 生成 PWM 脉冲

在这里调制就是指通过PWM输出呈正弦变化的电压。

个人理解

就已呼吸灯为例吧，在上一节我们说SPWM的时候，有一个图：

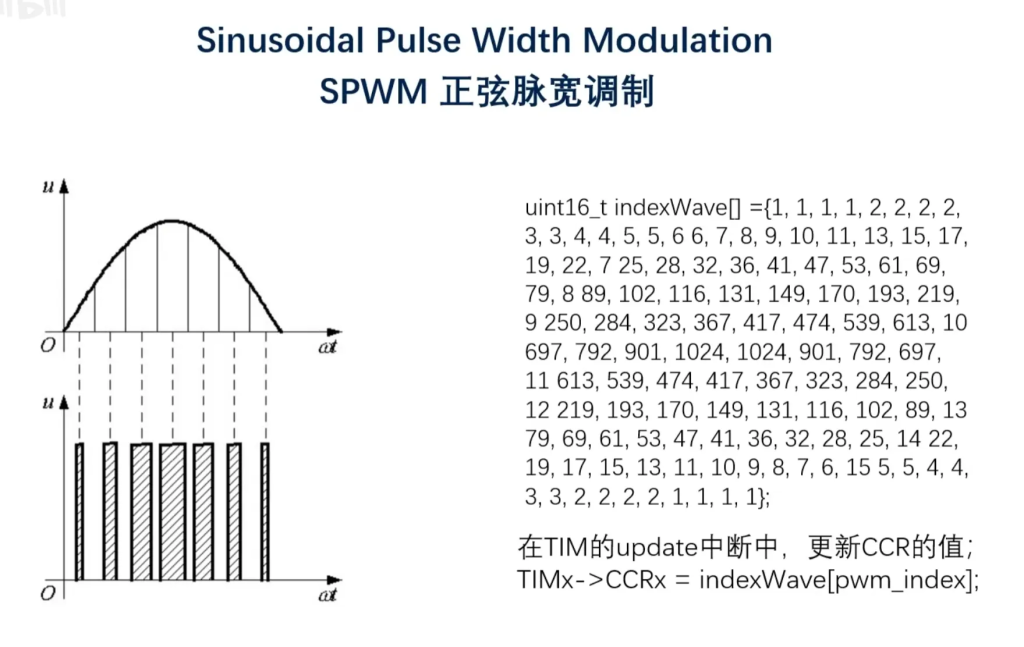
比如我们想让PWM占空比以正弦波的方式变换，从而使灯的亮度也按照正弦波的形式变换，于是我们就不断改变CCR的值，从而实现出图中下方所示的方波波形，这就是我们的调制波。

那么载波在哪里呢？在这之前，你还记得CCR是用来干什么的吗？是的，用来和计数器比较。那么计数器的值是一个三角波（通常情况下），这个三角波就是我们的载波频率了。（它又是来自于哪里呢？来自于定时器的工作时钟频率，也就是我们APB总线经过分频后的频率。虽然三角波是由于计数器以时钟频率计数产生的，但由于时钟频率并不直接参与调制，因此不能说是载波频率。）

2 数学形式：一条正弦，外加三次谐波

以三相系统为例，先给出最原始的“理想调制波”：

ua(t)ub(t)uc(t)=Umcos(ωt)=Umcos(ωt−120∘)=Umcos(ωt+120∘)

Um 由所需输出电压决定
ω=2πf，f 为期望输出频率（如 50 Hz）

但这样直接做 SPWM 时，最大基波幅值只能到 Vdc/2。为了榨干母线电压，工程上会给调制波注入三次谐波（或改用 SVPWM 等效实现），使波形变成“鞍形”——这就是你在 SVPWM 文献里看到的“调制波含有固定三次谐波含量”的来源。（SVPWM不是三次谐波注入！）

3 在硬件/软件里怎么产生这条“调制波”？

模拟实现
早期：用函数发生器或运放搭一个 50 Hz 正弦波 → 与三角波比较 → 输出 PWM。
数字实现（MCU/DSP）

查表法：预存 256 点或 512 点正弦表，按定时中断逐点输出。
实时计算：FOC/SVPWM 算法每个 PWM 周期实时计算下一拍的目标电压矢量，再反算出三相调制波瞬时值。
坐标变换：在 d-q 坐标系里运行 PI 调节器，得到 ud、uq，再经反 Park 变换回到三相调制波 ua,ub,uc。

一句话总结
调制波就是“用低频目标波形去指挥高频开关动作”的那条指令信号。
在电机控制里，它要么是一条纯正弦（SPWM），要么是经过空间矢量运算后的“鞍形”正弦（SVPWM）；无论哪种形式，最终目的都是让逆变器“雕刻”出我们想要的正弦电压。

SVPWM算法原理

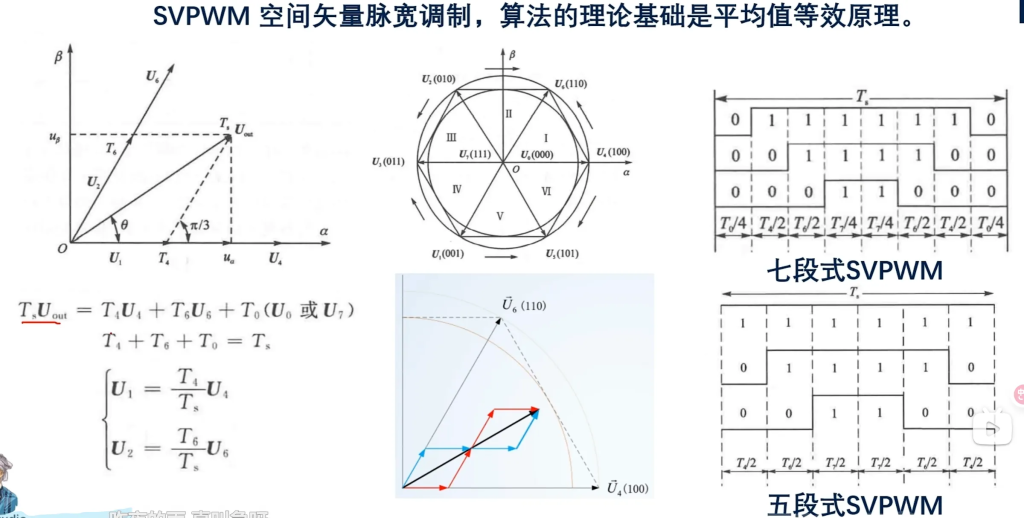
先看左边那部分，这部分说的是平均值等效原理。

$T_SU_{out} = T_4U_4 + T_6U_6 + T_0U_0(或U_7)$ ,

其中$T_s$是PWM周期，$T_s = T_4+T_6+T_0$；U4U6指中间上面的圆中不同方向的电压；而T0又是指“零序分量”：

零序分量（零区分量、共模分量）

这是什么东西？

在一个 PWM 周期内，为了让 两个有效矢量的时间之和 小于整个周期，而必须插入的那一段 零矢量（000 或 111）作用时间，以及它在三相端电压上产生的 共同抬高或拉低的电压成分。

为什么要插入这个东西？

为了保持PWM波形的对称性并减少谐波含量，通常会在非零电压空间矢量之间插入零电压空间矢量。零矢量的插入方式有多种，如中心对称插入、两端对称插入等。不同的插入方式会对电机的性能产生不同的影响。同时也为了保证“一次只切换一个管子”，需要在两次变换之间插入零区分量。

下面还有两个等式说明了U1、U2、U4、U6之间的关系。需要注意的是这里的U1U2不是指中间上面的圆中不同方向的电压，而是U4U6方向参与$U_{out}$合成的电压。也就是说，$U_{out}$是由U4U6这两个方向上的电压合成的，而U4和U6到底有多少参与了合成的具体数值则由这两个等式计算。

计算Uout最大值：过程

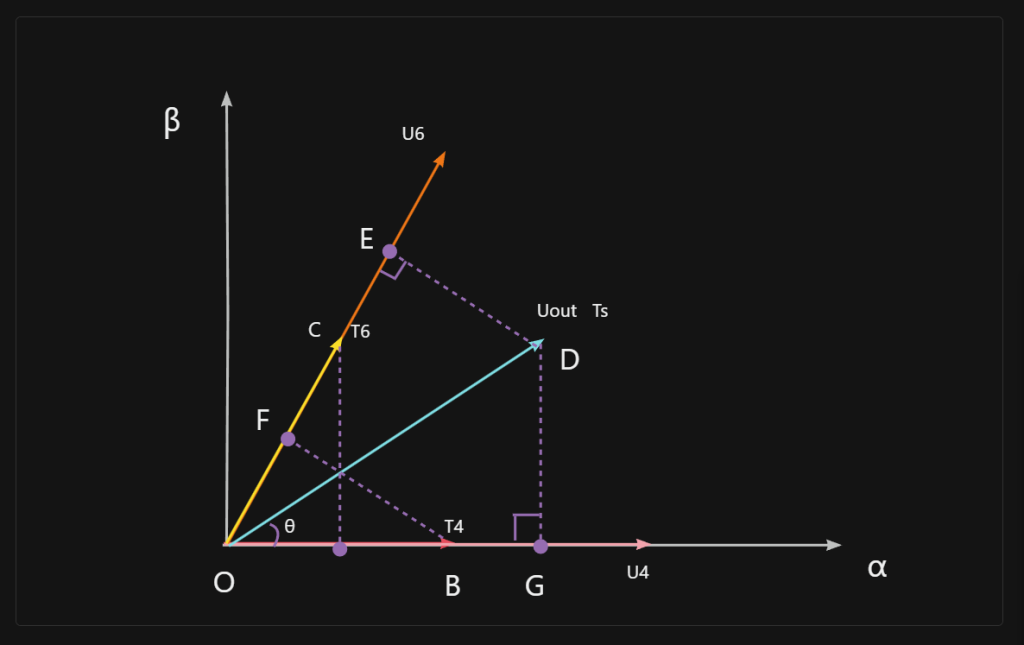
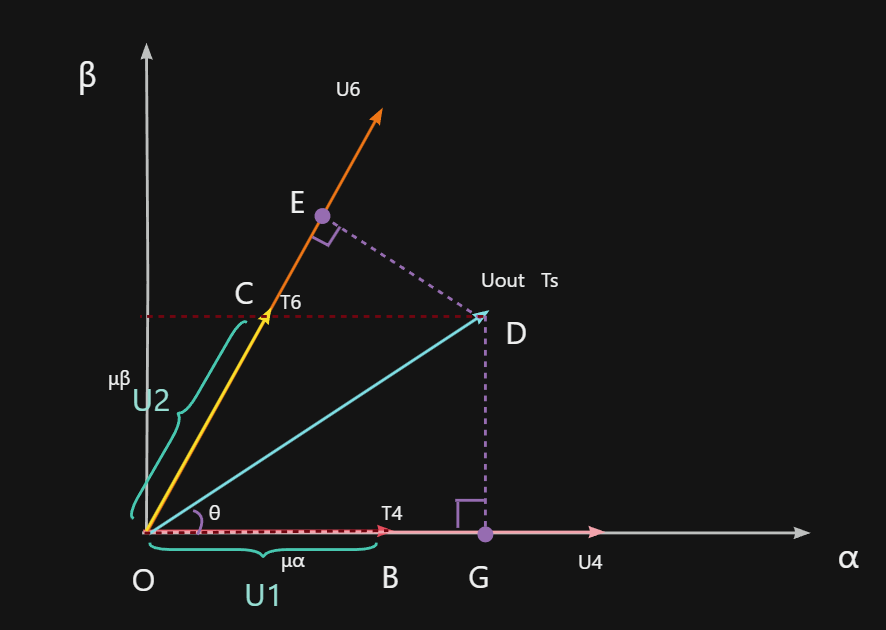
这是左上部分的图，并添加了点和辅助线方便描述计算过程。

首先我们有：$T_s = T_4+T_6+T_0$，也就是说$\frac{T_0+T_4+T_6}{T_s}=1$;

但是我们还不知道T0是多少，于是我们只能得到：$\frac{T_4+T_6}{T_s}<1$。

接下来我们来算算$T_{out}$的最大值：

作辅助线DE和BF，易得|DE|=|BF|；

又有：|DE| = $U_{out} · \sin (\frac{\pi}{3}-θ)$= |BF|；

所以：$T_4 · U_4$= $\frac{T_S·U_{out} · \sin (\frac{\pi}{3}-θ)}{\frac{\sqrt{3}}{2}}$,

同理，$T_6·U_6$= $\frac{T_S·U_{out} · \sinθ}{\frac{\sqrt{3}}{2}}$。

注：只要在这里稍稍移项便能得出$U_1$= $\frac{T_4}{T_s}U_4$。

将上面这两个式子中的U移到左边，并将两式相加（由于U6=U4，所以这里统一化为U4）：

$T_4 + T_6$= $\frac{T_S·U_{out} · (\sinθ+\sin (\frac{\pi}{3}-θ))}{\frac{\sqrt{3}}{2}U_{4}}$

=$\frac{T_S·U_{out} · (\sin (\frac{\pi}{3}+θ))}{\frac{\sqrt{3}}{2}U_{4}}$

将$T_s$移到左边，得：

$\frac{T_4+T_6}{T_s}$= $\frac{U_{out} · (\sin (\frac{\pi}{3}+θ))}{\frac{\sqrt{3}}{2}U_{4}}$

而又有：$\frac{T_4+T_6}{T_s}<1$，且$\sin (\frac{\pi}{3}+θ)$⋲ [$\frac{\sqrt 3}{2}$, 1 ]

所以：$U_{out} \le \frac{\sqrt3}{2}U_{4}$

不难发现，$\frac{\sqrt3}{2}U_{4}$正好是正六边形的内切圆的半径，也就是说，SVPWM能稳定在各个方向上输出的最大值就是$\frac{\sqrt3}{2}U_{4}$。

平均值等效原理

上面的计算过程需要一个前提：U4和U6同时存在。

但是现实里受到硬件限制我们没法做到这一点。因此我们就需要用到平均值等效原理（图中间下方部分）。

简单来说就是将整个过程拆分成一个个小过程，每个小过程中只存在U4或者U6，最终合成为输出值。

七段式和五段式SVPWM

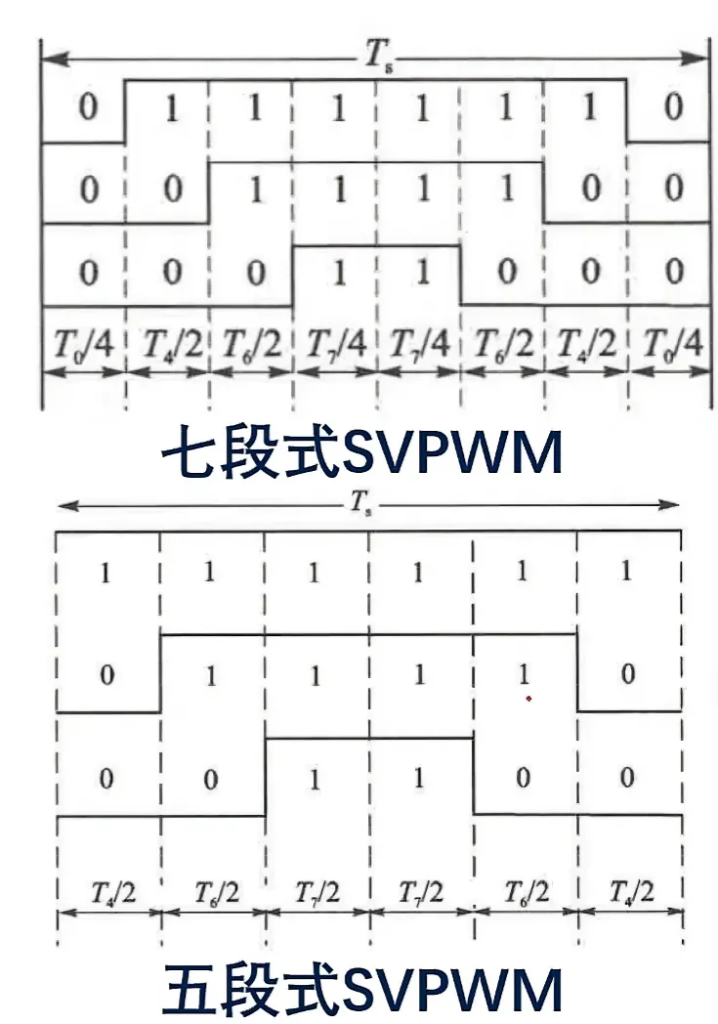
七段式和五段式主要差别在于零区分量的插入不同。

同时，从图中我们可以看到七段式mos管一共开关了6次（竖线），而五段式仅仅开关了4次。从开关损耗和截止损耗来看五段式更优。

但是减少/改变零区分量会导致五段式电流谐波比七段式多，因此两者各有优劣。

在实际中七段式用的最普遍，下文所说的都是以七段式为主。

电压矢量增量角

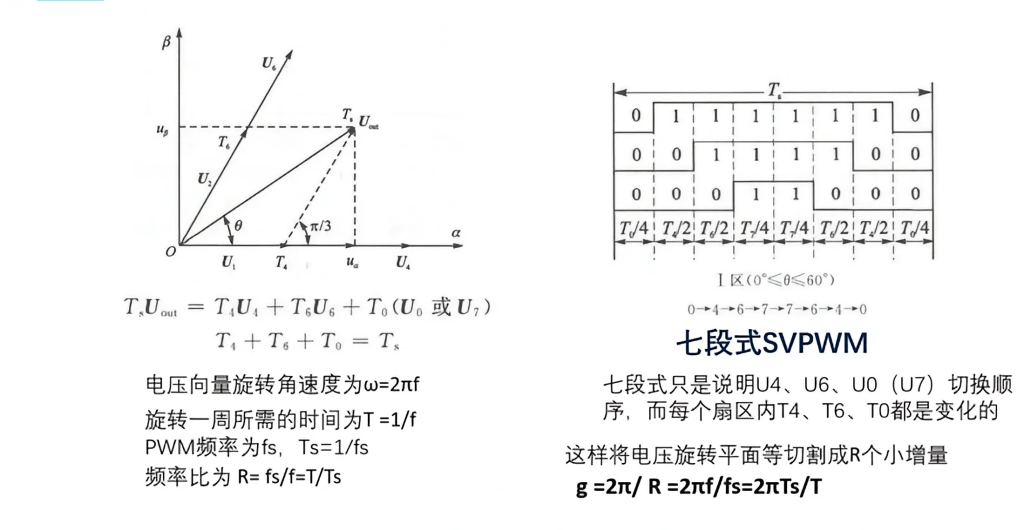
什么是电压矢量增量角

某一时刻，我们的$U_{out}$处在一个θ的角度下；经过$T_S$时刻后，$U_{out}$改变了它的角度。

那么这两个角度之差就是我们的增量角。

什么是“将电压旋转平面等切割成R个小增量”？

先看左边下方的说明，电压向量旋转一圈所需时间为T，我们两次PWM调制之间的间隔时间为Ts；所以在电压向量旋转一周的时间内，我们一共可以进行R=T/Ts次控制，也就是说我们可以把一个完整的圆等分成R个小扇形，每个小扇形角度为$g=\frac{2\pi}{R}=\frac{2\pi T_s}{T}$。g越小我们的控制就会越平滑，越大就越有段落感。

同时由于整个圆由六个基本电压分成6块大扇形，我们至少要保证g<60°才能使电机正常旋转。

七段式SVPWM控制流程：

确定当前电角度所在扇区
确定T4、T6(或其它扇区对应时间)大小
根据T4T6来计算CCR切换时间点
依照计算结果控制。

扇区判断

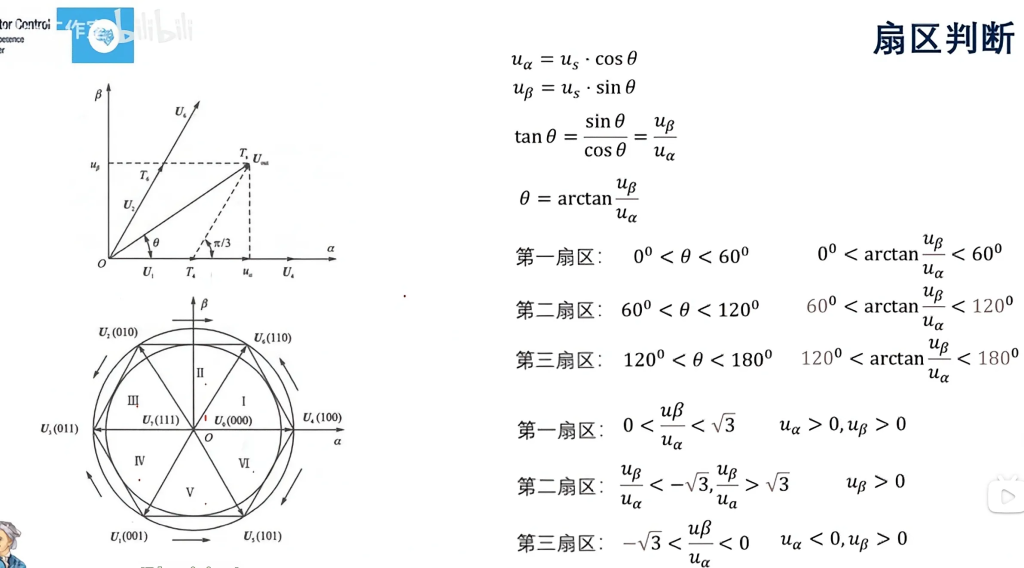
T4、T6计算

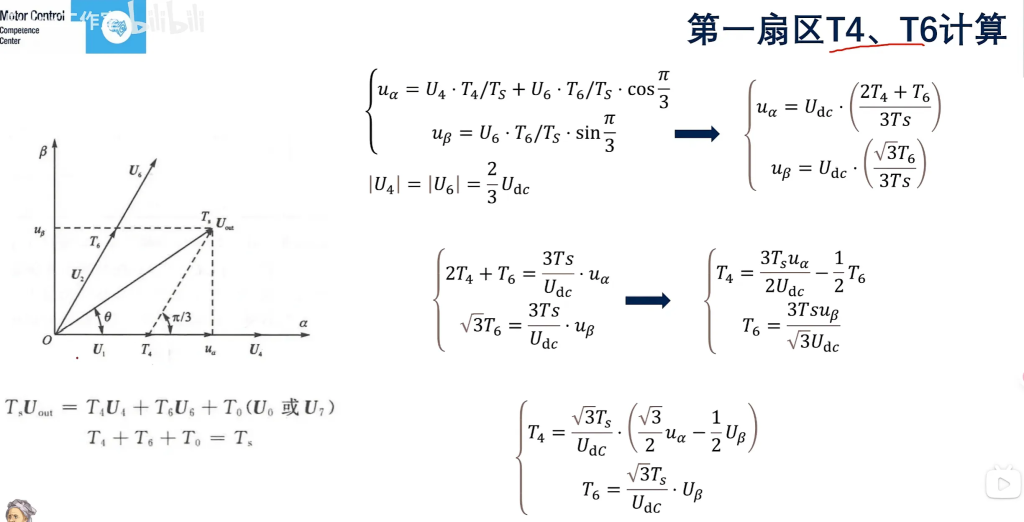
首先我们已知：$T_s · U_{out}=T_4U_4+T_6U_6+T_0U0(或U_7,下文同)$

移相得：$|U_{out}|=\frac{T_4}{T_s}|U_4|+\frac{T_6}{T_s}|U_6|+\frac{T_0}{T_s}|U0|$

而且易得：$\frac{T_4}{T_s}|U_4|=|U_1|$,$\frac{T_6}{T_s}|U_6|=|U_2|$

我们又是知道∠COB=60°，所以有：

$$\begin{cases}\mu\alpha=U_1+U_2·\cos\frac{\pi}{3} \\mu\beta=U_2·\sin\frac{\pi}{3} \ \end{cases}$$

又因为：$|U_4|=|U_6|=\frac{2}{3}|U_dc|$,

为什么$|U_4|=|U_6|=\frac{2}{3}|U_dc|$？

这是由于电路内部结构决定每一项的相电压最大只能达到$\frac{2}{3}U_dc$,$U_4、U_6$虽然是合成矢量，但由于两相间夹角120°，刚好使合成后数值不变。

所以：

$$\begin{cases} u_\alpha = U_{\text{dc}} \cdot \\ (\frac{2 T_4 + T_6}{3 T_s}) \ u_\beta = U_{\text{dc}} \cdot (\frac{\sqrt{3} T_6}{3 T_s}) \end{cases}$$

再经过一系列移相、通分：

$$\begin{cases} T_4 = \frac{\sqrt{3} T_s}{U_{dc}}\\ \cdot (\frac{\sqrt{3}}{2} u_\alpha – \frac{1}{2} U_\beta) \ T_6 = \frac{\sqrt{3} T_s}{U_{dc}} \cdot U_\beta \end{cases}$$

总结

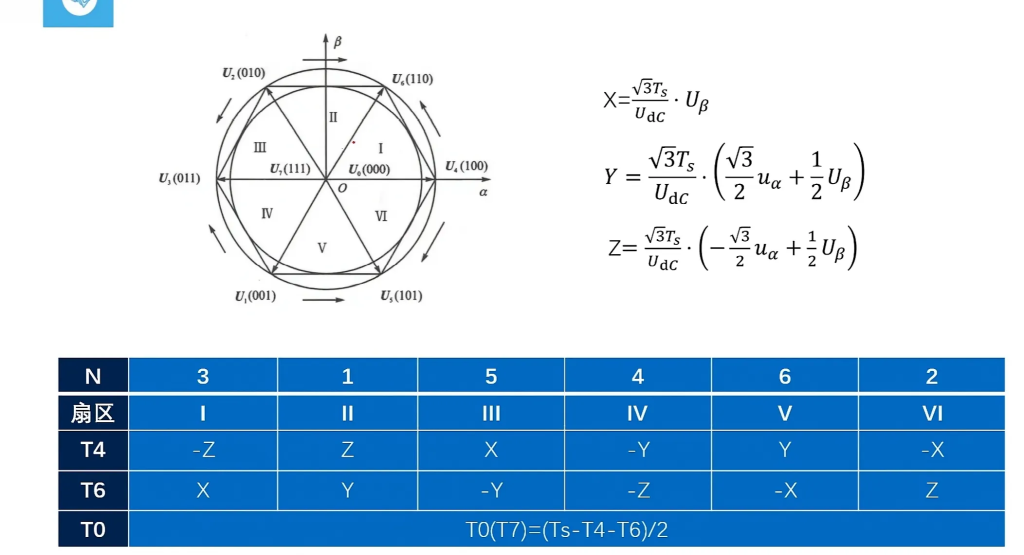
N	3	1	5	4	6	2
扇区	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ
T4	-Z	Z	X	-X	-Y	Y
T6	X	Y	-Y	Z	-Z	-X
T0=T7=(Ts-T4-T6)/2

什么是T4、T6？

看见圆外面的箭头了吗？每个箭头从“U4”出发，指向“U6”。比如在第二扇区里，“U4”为U2，“U6”为U6 。

另外注意括号里的部分，并与判断扇区时用到的$U_{ref2}、U_{ref3}$比较，可以发现两者相等。因此可以减小一些计算量。

实际写代码时不用分的太清这两者的区别，因为下文计算切换时刻时还有一个判断；在这一步我们只要把XYZ计算好并按表格赋值给T4T6就行了。

mos管切换时刻（Ⅰ、Ⅱ区为例）

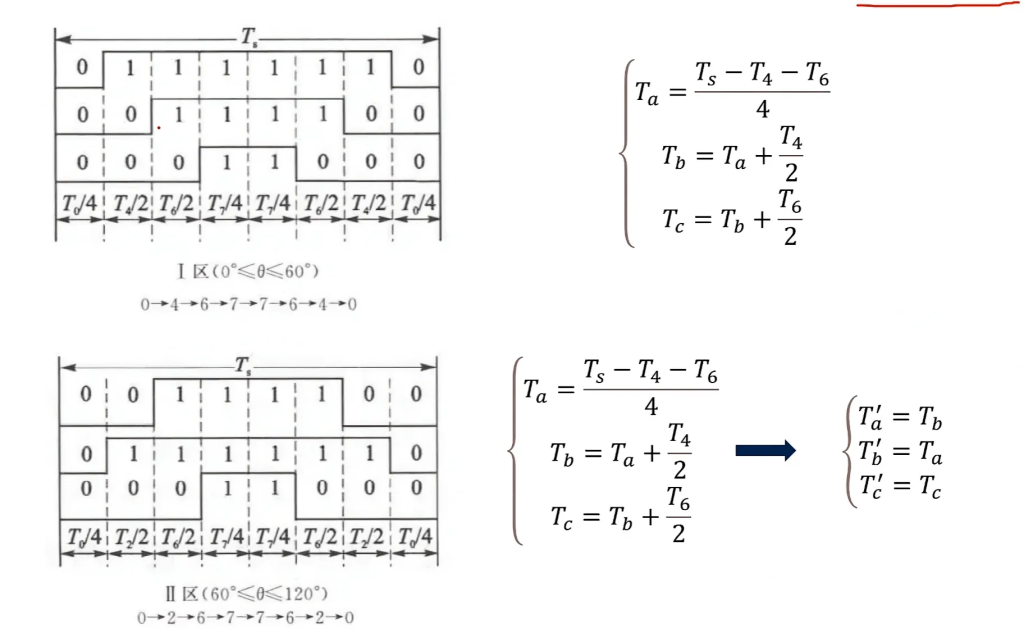
切换时刻，是指在一段完整的七段式周期中应该在何时开关对应的mos管。

三条折线从上到下分别对应a、b、c三相，因此我们把切换对应相的时刻称为Ta、Tb、Tc。

又因为周期是对称的，因此我们只要让定时器采取中心对齐计数，便可以免去计算两次的麻烦。

第Ⅰ扇区右边的计算不难看懂；但是第Ⅱ扇区右边因为排版原因有些难以理解：

左边括号里的TaTbTc对应的是第Ⅰ扇区计算出来的值，$T_a^\prime T_b^\prime T_c^\prime$才是第Ⅱ扇区的值。

看到这你应该也能看出来，在一个周期内，一共有6个切换时间点，而他们两两对称，所以我们关心的只有三个时间点；这三个时间点的值是“固定”的，不同扇区只是每个时间点对应切换的MOS管不同而已。

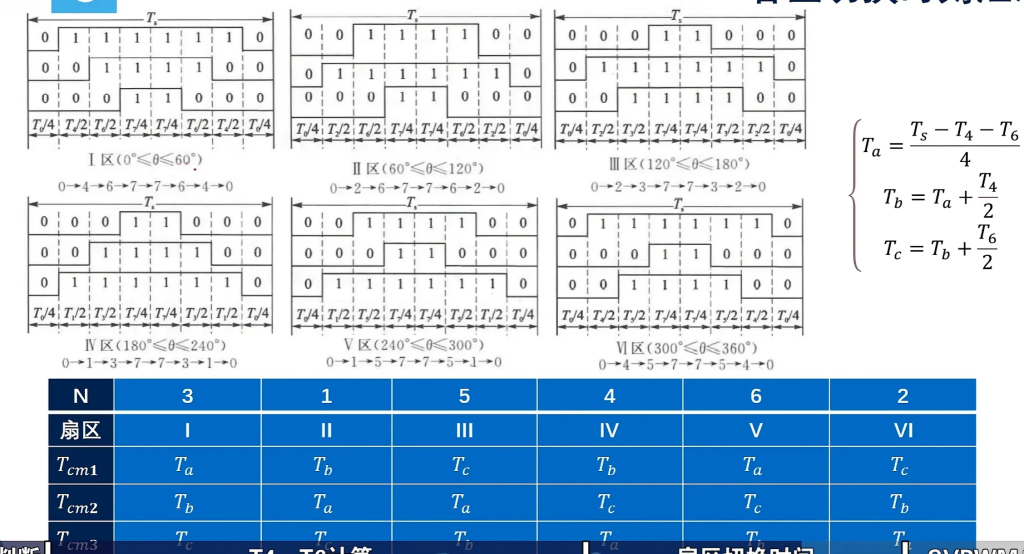
这是怎么编排的？

一个七段式周期可分为8个部分，我们看前四个部分。不难发现不论在哪个扇区，第一部分永远是3个0，第二部分是3个0一个1，第三部分是2个0一个1，第四部分是3个1 。通过以含有1的个数对各相排序，可以保证一次只切换一个mos管。

采样问题

我们希望在周期中心时刻对电路进行电流采样，而想要采样有必须在电路下桥打开时才能进行。可是当我们处于周期中间时，所有路全是“1”，也就是上桥打开。这怎么办呢？

我们只要稍稍改变各路切换顺序，比如让1多的先出现。以Ⅰ区为例，原先的切换顺序是04677640，但我们改编成76400467，就可以保证周期中间时对下桥采样了。而且这么做我们也不需要重新计算切换时间，只需要将计时器计数方式从“/\”改为“\/”就行了，实际上就是改变了三角波的相位。（后记：视频演示里是改变了切换顺序的，但原理相同。）

仿真

代码接收Uα、Uβ、Udc和Ts的值，输出3路切换时间点和当前扇区。

文中的T1T2即为T4T6，Tpwm为Ts。

single(0)表示单精度0，即C里的float类型。

C

function [Tcmp1,Tcmp2,Tcmp3,sector] = fcn(Valpha,Vbeta,Udc,Tpwm)
%#codegen

sector = single(0);
Tcmp1 = single(0);
Tcmp2 = single(0);
Tcmp3 = single(0);

%========Parameters statement================

    Vref1 = Vbeta;							                   
    Vref2 = (sqrt(3)*Valpha - Vbeta)/2; 				    
    Vref3 = (-sqrt(3)*Valpha - Vbeta)/2;					
   
 %========Sector calculation=================

  if (Vref1>0)
	   sector = single(1);
  end
  if (Vref2>0)
	   sector = sector+single(2);
  end
  if (Vref3>0)
       sector = sector+single(4);
  end

%======== X Y Z calculation===================

X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);	         

%==========Duty ratio calculation================
switch (sector)   
    case 1
        T1 = Z; T2 = Y; 
	case 2
        T1 = Y; T2 = -X; 
	case 3
        T1 = -Z; T2 = X; 
	case 4
        T1 = -X; T2 = Z;
	case 5
        T1 = X; T2 = -Y;
    otherwise
        T1 = -Y; T2 = -Z;
end

if T1+T2 > Tpwm
    T1 = T1/(T1+T2);
    T2 = T2/(T1+T2);
end

ta = (Tpwm-(T1+T2))/4.0;
tb = ta+T1/2;
tc = tb+T2/2;

%==========Duty ratio calculation================
switch (sector)
    case 1 
        Tcmp1=tb;
        Tcmp2=ta;
        Tcmp3=tc; 
        
    case 2 
        Tcmp1=ta;
        Tcmp2=tc;
        Tcmp3=tb; 
       
    case 3 
        Tcmp1=ta;
        Tcmp2=tb;
        Tcmp3=tc; 
        
    case 4 
        Tcmp1=tc;
        Tcmp2=tb;
        Tcmp3=ta;
        
    case 5 
        Tcmp1=tc;
        Tcmp2=ta;
        Tcmp3=tb;
        
   case 6
       Tcmp1=tb;
       Tcmp2=tc;
       Tcmp3=ta;
end
end

function [Tcmp1,Tcmp2,Tcmp3,sector] = fcn(Valpha,Vbeta,Udc,Tpwm)
%#codegen

sector = single(0);
Tcmp1 = single(0);
Tcmp2 = single(0);
Tcmp3 = single(0);

%========Parameters statement================

    Vref1 = Vbeta;							                   
    Vref2 = (sqrt(3)*Valpha - Vbeta)/2; 				    
    Vref3 = (-sqrt(3)*Valpha - Vbeta)/2;					
   
 %========Sector calculation=================

  if (Vref1>0)
	   sector = single(1);
  end
  if (Vref2>0)
	   sector = sector+single(2);
  end
  if (Vref3>0)
       sector = sector+single(4);
  end

%======== X Y Z calculation===================

X = sqrt(3)*Vbeta*Tpwm/Udc;
Y = Tpwm/Udc*(3/2*Valpha+sqrt(3)/2*Vbeta);
Z = Tpwm/Udc*(-3/2*Valpha+sqrt(3)/2*Vbeta);	         

%==========Duty ratio calculation================
switch (sector)   
    case 1
        T1 = Z; T2 = Y; 
	case 2
        T1 = Y; T2 = -X; 
	case 3
        T1 = -Z; T2 = X; 
	case 4
        T1 = -X; T2 = Z;
	case 5
        T1 = X; T2 = -Y;
    otherwise
        T1 = -Y; T2 = -Z;
end

if T1+T2 > Tpwm
    T1 = T1/(T1+T2);
    T2 = T2/(T1+T2);
end

ta = (Tpwm-(T1+T2))/4.0;
tb = ta+T1/2;
tc = tb+T2/2;

%==========Duty ratio calculation================
switch (sector)
    case 1 
        Tcmp1=tb;
        Tcmp2=ta;
        Tcmp3=tc; 
        
    case 2 
        Tcmp1=ta;
        Tcmp2=tc;
        Tcmp3=tb; 
       
    case 3 
        Tcmp1=ta;
        Tcmp2=tb;
        Tcmp3=tc; 
        
    case 4 
        Tcmp1=tc;
        Tcmp2=tb;
        Tcmp3=ta;
        
    case 5 
        Tcmp1=tc;
        Tcmp2=ta;
        Tcmp3=tb;
        
   case 6
       Tcmp1=tb;
       Tcmp2=tc;
       Tcmp3=ta;
end
end

9 月 5, 2025

—

由

文止墨

于嵌入式, 文章, 编程

文于止墨

STM32G0/G4驱动BLDC/PMSM电机——第六讲：SVPWM

SPWM和SVPWM介绍

控制逻辑

矢量合成

SVPWM算法原理

什么是调制比？