前言
文章基本思路来自:James Routley
其中,判断点是否在多边形内的算法来自:PNPOLY – Point Inclusion in Polygon Test – WR Franklin (WRF)
本代码中的颜色来自于:RGB颜色值与十六进制颜色码转换工具,并使用 RGB与十六进制与RGB565颜色转换工具 转换为RGB565代码。(坦白说,我还挺喜欢这些颜色的,比莫奈色系要更鲜艳一点)
想要实现本文代码,你至少需要有如下功能的函数:绘制直线、绘制点、随机数。
Terazzo 是一种通过将小的彩色碎屑粘合在水泥中制成的材料。凝固后,对其进行切割和抛光,露出由木屑制成的图案。
它在用为装饰性随机背景时有不错的表现。
原理:通过随机产生不重叠的圆,并在圆内内接一个多边形,即可确保生成的多边形是凸多边形且互不交叉。
图为原理演示图。由于画圆函数无法正确处理负数坐标,出现了重叠的情况。

以及它的最终效果看起来是这样的:

下面是代码:
terazzo.h
#ifndef TERAZZO_H
#define TERAZZO_H
#include "./BSP/LCD/lcd.h"
#include "./SYSTEM/sys/sys.h"
#include <stdlib.h>
#include <math.h>
#include <stdio.h>
#define Pink 0xfe19 //粉色
#define LavenderBlush 0xff9e //脸红的淡紫色
#define Thistle 0xddfb //蓟
#define MediumSlateBlue 0x7b5d //适中的板岩暗蓝灰色
#define Lavender 0xe73f //熏衣草花的淡紫色
#define CornflowerBlue 0x64bd //矢车菊的蓝色
#define LightSteelBlue 0xb63b //淡钢蓝
#define LightCyan 0xe7ff //淡青色
#define Auqamarin 0x7ff5 //绿玉\碧绿色
#define Khaki 0xf731 //卡其布
#define Moccasin 0xff36 //鹿皮鞋
#define LightSalmon 0xfd0f //浅鲜肉(鲑鱼)色
#define LightCoral 0xf410 //淡珊瑚色
typedef struct {
uint8_t r;
uint16_t x;
uint16_t y;
}Circle;
extern uint16_t terazzo_COLORS[13];
/*清空画布*/
void init_terazzo(void);
/* 在指定大小的画布内(尽可能地)画指定数量的多边形 */
void update_terazzo(uint16_t width,uint16_t height,uint16_t num);
#endif
terazzo.c
#include "./BSP/terazzo/terazzo.h"
Circle c[150]={0}; //圆集合
uint16_t cnum=0; //圆个数
uint16_t terazzo_COLORS[13]={Pink,LavenderBlush,Thistle,MediumSlateBlue,Lavender,CornflowerBlue,LightSteelBlue,LightCyan,Auqamarin,Khaki,Moccasin,LightSalmon,LightCoral};
uint16_t p_width=320,p_height=480; //画布宽度
void init_terazzo(void){
//c={0};
cnum=0;
lcd_clear(g_back_color);
}
int terazzo_Random(int n)
{
srand(SysTick->VAL+n); /* 半主机模式下使用time函数会报错,在这里用系统定时器的值替代 */
return rand() % 1000;
}
int check_circle(Circle *circle){
for(int i=0;i<cnum;i++){
int x=circle->x-c[i].x;
int y=circle->y-c[i].y;
if((x*x+y*y)<pow(circle->r+c[i].r,2)){
//printf("0");
return 0;
}
}
//printf("check_success\n");
return 1;
}
/*
返回一个不与其它圆重叠的圆,如果返回的圆半径为0,说明找不到这种圆
*/
Circle create_circle(){
Circle cir;
int r=0;
do{
cir.r=terazzo_Random(r+=10)%45+10;
cir.x=terazzo_Random(r+=10)%p_width;
cir.y=terazzo_Random(r+=10)%p_height;
}while(!check_circle(&cir)&&(r<3000));
if(!check_circle(&cir)){
//printf("creat_error\n");
cir.r=0;
}
//printf("\n%d %d\n",cir.x,cir.y);
//printf("creat_success\n");
return cir;
}
/*
填充指定圆里的多边形,采用逐行扫描填充算法,圆的边界坐标用勾股定理获得。
(Bresenham算法没学会)
按照从左到右、从上到下的方法扫描
注意,本函数的边界判断有很大漏洞。
*/
void terazzo_scan_fill_color(Circle cir,uint16_t color){
for(int i=0;i<=cir.r;i++){
if(i<0)i=0;
if(i>=p_width)i=p_width-1;
int h =sqrt(cir.r*cir.r-pow(cir.r-i,2)); //计算扫描长度
uint8_t last_point = 0;
uint8_t b = 0;
for(int j=cir.y-h;j<cir.y+h;j++){ //左边
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x-cir.r+i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(lcd_read_point(tx,ty)==color){ //扫描到彩色
if(!last_point){ //上一个点不是彩色,说明这个点是边界
b=!b; //切换填色
last_point=1;
}
}else{
last_point=0;
}
if(b){
lcd_draw_point(cir.x-cir.r+i,j,color);
}
}
b = 0;
last_point = 0;
for(int j=cir.y-h;j<cir.y+h;j++){ //右边
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x+cir.r-i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(lcd_read_point(tx,ty)==color){ //扫描到彩色
if(!last_point){//上一个点不是彩色,说明这个点是边界
b=!b; //切换填色
last_point=1;
}
}else{
last_point=0;
}
if(b){
lcd_draw_point(cir.x+cir.r-i,j,color);
}
}
printf("fill,%d\n",h);
}
}
/*此算法由W. Randolph Franklin提出*/
/*参考链接:https://wrfranklin.org/Research/Short_Notes/pnpoly.html*/
uint8_t terazzo_pnpoly(int nvert, uint16_t *vertx, uint16_t *verty, uint16_t testx, uint16_t testy)
{
uint16_t i, j, c = 0;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
if ( ((verty[i]>testy) != (verty[j]>testy)) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
c = !c;
}
return c;
}
/*
采用判断点是否在多边形的内部,从而上色。
nvert:顶点数
vertx/y:存有顶点坐标的数组
*/
void terazzo_vector_fill_color(Circle cir,uint16_t color,uint8_t nvert, uint16_t *vertx, uint16_t *verty){
for(int i=0;i<=cir.r*cir.r;i++){
int h =sqrt(cir.r*cir.r-pow(cir.r-i,2)); //计算扫描长度
for(int j=cir.y-h;j<=cir.y+h;j++){
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x+cir.r-i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(OLED_pnpoly(nvert,(short *)vertx,(short *)verty,tx,j)){
//printf("");
lcd_draw_point(tx,j,color);
}
}
}
}
/*
在一个给定的圆里选取随机的点,并按指定的颜色连线
内部连线方式:先随机产生3~6个弧度值,并按大小排序。
然后按照排序顺序生成点坐标并连线。
这样可以确保生成的连线不会交叉。
*/
void link_point(Circle *cir,uint16_t color){
if(cir->r==0){
//printf("draw_error\n");
return;
}
int zeta_num = terazzo_Random(cir->x+cir->y) % 5 + 3;
float zeta[zeta_num];
for(int i=0;i<zeta_num;i++){
zeta[i] = terazzo_Random(i+cir->x+cir->y)%628/100.0f;//生成弧度值
}
/* 选择排序,小的在前 */
for(int i=0;i<zeta_num;i++){
int z=zeta_num-1;
for(int j=zeta_num-1;j>=i;j--){
if(zeta[z]>zeta[j]){
z=j;
}
}
float t=zeta[i];
zeta[i]=zeta[z];
zeta[z]=t;
}
int16_t pointx[zeta_num],pointy[zeta_num];
/* 生成点坐标 */
for(int i=0;i<zeta_num;i++){
pointx[i]=(cir->x-cir->r*cos(zeta[i]));
pointy[i]=(cir->y-cir->r*sin(zeta[i]));
if(pointx[i]>=p_width){
pointx[i]=p_width-1;
}
if(pointy[i]>=p_height){
pointy[i]=p_height-1;
}
if(pointx[i]<0){
pointx[i]=0;
}
if(pointy[i]<0){
pointy[i]=0;
}
}
/* 连线 */
for(int i=0;i<zeta_num;i++){
lcd_draw_line(pointx[i],pointy[i],pointx[(i+1)%zeta_num],pointy[(i+1)%zeta_num],color);
}
terazzo_vector_fill_color(*cir,color,zeta_num,(uint16_t *)pointx,(uint16_t *)pointy);
//lcd_draw_circle(cir->x,cir->y,cir->r,RED);
c[cnum++]=*cir;
//printf("draw:%d\n",cnum);
}
/*
在指定大小的画布内(尽可能地)画指定数量的多边形
`*/
void update_terazzo(uint16_t width,uint16_t height,uint16_t num){
p_width=width;
p_height=height;
Circle cir;
for(int i=0;i<num;i++){
cir=create_circle();
link_point(&cir,terazzo_COLORS[terazzo_Random(i)%13]);
}
printf("%d\n",cnum);
}
函数详解:
int check_circle(Circle *circle);
int check_circle(Circle *circle){
for(int i=0;i<cnum;i++){
int x=circle->x-c[i].x;
int y=circle->y-c[i].y;
if((x*x+y*y)<pow(circle->r+c[i].r,2)){
return 0;
}
}
return 1;
}勾股定理算圆心距离,与半径和比较判断两圆位置关系。
Circle create_circle();
/*
返回一个不与其它圆重叠的圆,如果返回的圆半径为0,说明找不到这种圆
*/
Circle create_circle(){
Circle cir;
int r=0;
do{
cir.r=terazzo_Random(r+=10)%45+10;
cir.x=terazzo_Random(r+=10)%p_width;
cir.y=terazzo_Random(r+=10)%p_height;
}while(!check_circle(&cir)&&(r<3000));
if(!check_circle(&cir)){
cir.r=0;
};
return cir;
}创建一个圆并检查它是否与其它圆相交,直到找到一个满足条件的圆为止;或是重复一定次数为止,此时返回半径为0的圆表示这种圆未找到。
void terazzo_scan_fill_color(Circle cir,uint16_t color);
/*
填充指定圆里的多边形,采用逐行扫描填充算法,圆的边界坐标用勾股定理获得。
(Bresenham算法没学会)
按照从左到右、从上到下的方法扫描
注意,本函数的边界判断有很大漏洞。
*/
void terazzo_scan_fill_color(Circle cir,uint16_t color){
for(int i=0;i<=cir.r;i++){
if(i<0)i=0;
if(i>=p_width)i=p_width-1;
int h =sqrt(cir.r*cir.r-pow(cir.r-i,2)); //计算扫描长度
uint8_t last_point = 0;
uint8_t b = 0;
for(int j=cir.y-h;j<cir.y+h;j++){ //左边
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x-cir.r+i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(lcd_read_point(tx,ty)==color){ //扫描到彩色
if(!last_point){ //上一个点不是彩色,说明这个点是边界
b=!b; //切换填色
last_point=1;
}
}else{
last_point=0;
}
if(b){
lcd_draw_point(cir.x-cir.r+i,j,color);
}
}
b = 0;
last_point = 0;
for(int j=cir.y-h;j<cir.y+h;j++){ //右边
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x+cir.r-i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(lcd_read_point(tx,ty)==color){ //扫描到彩色
if(!last_point){//上一个点不是彩色,说明这个点是边界
b=!b; //切换填色
last_point=1;
}
}else{
last_point=0;
}
if(b){
lcd_draw_point(cir.x+cir.r-i,j,color);
}
}
}
}
注意,本函数的边界检测有问题,即不能很好的判断点是否在边界内部;
效果大体是这样的……
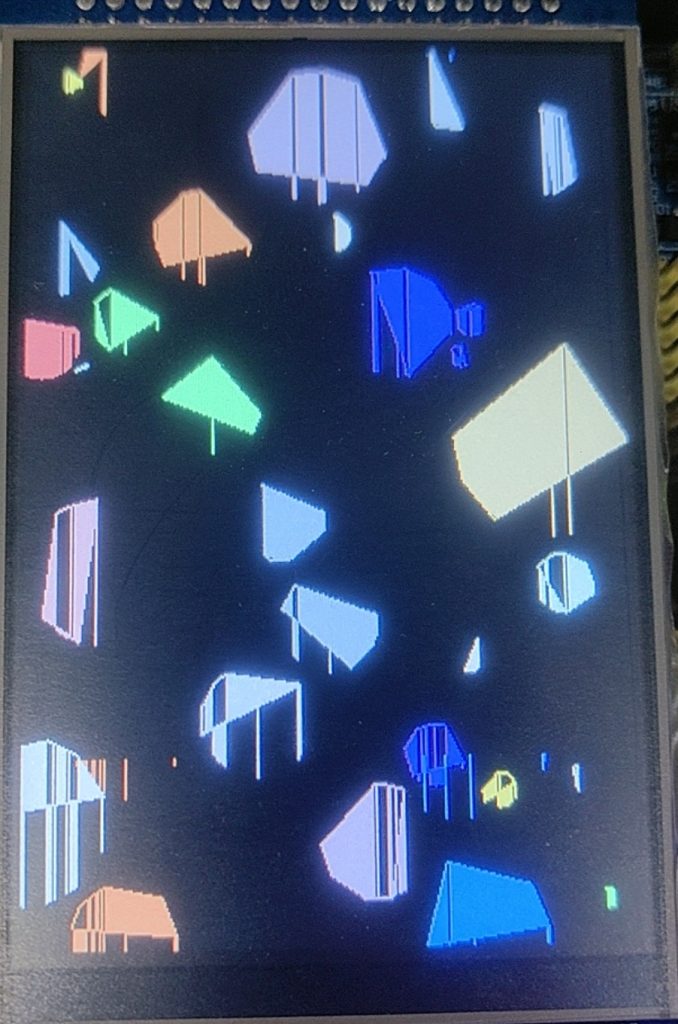
整体思路:类似逐行扫描法,逐列的从上至下扫描多边形所在的圆;
函数维护两个变量:上个点的状态(last_point)、现在是否可以绘图(b);
当我们扫描到某点时发现它是“彩色的”(即颜色与指定颜色相同),于此同时,上一点不是彩色的——这就说明我们扫描到的这一点为边界点,可以开始绘画了;如果上一点是彩色的,说明此时仍然在边界中(因为有的图形会形成竖直的边)。当我们在同一列里再次扫描到边界时退出绘画模式。
从逻辑上看,算法有如下问题:当图形比较尖锐时,完全有可能一列只包含一个点(顶点),此时由于检测不到第二个边界就会将这一列剩下的部分填满
从事实看感觉问题远不止如此……但我想不明白为什么……
uint8_t terazzo_pnpoly(int nvert, uint16_t *vertx, uint16_t *verty, uint16_t testx, uint16_t testy);
/*此算法由W. Randolph Franklin提出*/
/*参考链接:https://wrfranklin.org/Research/Short_Notes/pnpoly.html*/
uint8_t terazzo_pnpoly(int nvert, uint16_t *vertx, uint16_t *verty, uint16_t testx, uint16_t testy)
{
uint16_t i, j, c = 0;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
if ( ((verty[i]>testy) != (verty[j]>testy)) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
c = !c;
}
return c;
}看文章就好了,请自带翻译器。该网站还收录了关于计算机图形学的其它问题,有实力的大佬建议去看看~
void terazzo_vector_fill_color(Circle cir,uint16_t color,uint8_t nvert, uint16_t *vertx, uint16_t *verty);
/*
采用判断点是否在多边形的内部,从而上色。
nvert:顶点数
vertx/y:存有顶点坐标的数组
*/
void terazzo_vector_fill_color(Circle cir,uint16_t color,uint8_t nvert, uint16_t *vertx, uint16_t *verty){
for(int i=0;i<=cir.r*cir.r;i++){
int h =sqrt(cir.r*cir.r-pow(cir.r-i,2)); //计算扫描长度
for(int j=cir.y-h;j<=cir.y+h;j++){
int ty = j;
if(ty<0)ty=0;
if(ty>=p_height)ty=p_height-1; //判断是否越界
int tx=cir.x+cir.r-i;
if(tx<0)tx=0;
if(tx>=p_width)tx=p_width-1;
if(OLED_pnpoly(nvert,(short *)vertx,(short *)verty,tx,j)){
lcd_draw_point(tx,j,color);
}
}
}
}主要注意的是对ty和tx的预处理:由于正点原子给的驱动函数并不能很好的处理负数坐标,所以我对所有程序生成的坐标都做了边界处理,同时修改了驱动代码以使其在绘制的时候可以跳过那些不合理的坐标。
void link_point(Circle *cir,uint16_t color);
/*
在一个给定的圆里选取随机的点,并按指定的颜色连线
内部连线方式:先随机产生3~6个弧度值,并按大小排序。
然后按照排序顺序生成点坐标并连线。
这样可以确保生成的连线不会交叉。
*/
void link_point(Circle *cir,uint16_t color){
if(cir->r==0){
//printf("draw_error\n");
return;
}
int zeta_num = terazzo_Random(cir->x+cir->y) % 5 + 3;
float zeta[zeta_num];
for(int i=0;i<zeta_num;i++){
zeta[i] = terazzo_Random(i+cir->x+cir->y)%628/100.0f;//生成弧度值
}
/* 选择排序,小的在前 */
for(int i=0;i<zeta_num;i++){
int z=zeta_num-1;
for(int j=zeta_num-1;j>=i;j--){
if(zeta[z]>zeta[j]){
z=j;
}
}
float t=zeta[i];
zeta[i]=zeta[z];
zeta[z]=t;
}
int16_t pointx[zeta_num],pointy[zeta_num];
/* 生成点坐标 */
for(int i=0;i<zeta_num;i++){
pointx[i]=(cir->x-cir->r*cos(zeta[i]));
pointy[i]=(cir->y-cir->r*sin(zeta[i]));
if(pointx[i]>=p_width){
pointx[i]=p_width-1;
}
if(pointy[i]>=p_height){
pointy[i]=p_height-1;
}
if(pointx[i]<0){
pointx[i]=0;
}
if(pointy[i]<0){
pointy[i]=0;
}
}
/* 连线 */
for(int i=0;i<zeta_num;i++){
lcd_draw_line(pointx[i],pointy[i],pointx[(i+1)%zeta_num],pointy[(i+1)%zeta_num],color);
}
terazzo_vector_fill_color(*cir,color,zeta_num,(uint16_t *)pointx,(uint16_t *)pointy);
//lcd_draw_circle(cir->x,cir->y,cir->r,RED);
c[cnum++]=*cir;
}
值得注意的是对生成的弧度值进行排序:这是为了防止在连线的时候生成形如沙漏的自交叉的多边形。
如果你不想生成过于细长的形状,可以在函数第16行改为【上一次产生的弧度值+随机值+合适的常数】来规定两个点之间的最小距离。注意别超过2Π。
void update_terazzo(uint16_t width,uint16_t height,uint16_t num);
/*
在指定大小的画布内(尽可能地)画指定数量的多边形
`*/
void update_terazzo(uint16_t width,uint16_t height,uint16_t num){
p_width=width;
p_height=height;
Circle cir;
for(int i=0;i<num;i++){
cir=create_circle();
link_point(&cir,terazzo_COLORS[terazzo_Random(i)%13]);
}
printf("%d\n",cnum);
}整个文件唯二的接口之一(另一个是初始化函数)它规定了程序该在什么范围画图,应该画多少个形状。
不过由于随机性,通常程序生成的图案个数都比指定的小。
同时,由于单片机内存的限制,大于150的数字是无意义的。(我没做数组的边界检查,所以大于这个数一定会产生出乎意料的错误)
结尾:
本来想在网页里内嵌一个js脚本来直接生成一个可以被用户复制的图的,结果因为本人不懂前端而放弃了。
不过通过前言里的网址也能达到同样的效果!

发表回复